Exercícios de Mudança para Coordenadas Cilíndricas - Lista de Exercícios Resolvida
Questão 1
Seja a região interior à esfera que satisfaz e .
- Descreva em coordenadas cilíndricas.
- Supondo que a densidade é , determine a massa .
Questão 4
Calcule a integral tripla
Onde é a região limitada pelas superfícies de equações e .
Ver solução completaQuestão 5
Determine o volume do sólido , que está contido no cilindro , abaixo do plano e acima do paraboloide .
Ver solução completaQuestão 6
Calcule, usando integração, o volume do sólido limitado pelas superfícies , e .
Ver solução completaQuestão 7
Calcule, usando integração, o volume do sólido limitado pelas superfícies , e .
Dica: .
Ver solução completaQuestão 9
O volume do sólido interno ao cilindro , e limitado pelas superfícies e é:
Escolha uma:
a)
b)
c)
d)
e)
Ver solução completaQuestão 10
Calcule a integral tripla
Onde é a região limitada pelas superfícies de equações e .
Ver solução completaQuestão 11
4. Seja o sólido interior ao cone abaixo do plano e considere a integral
a) Forneça uma expressão para em coordenadas cilíndricas.
Ver solução completaQuestão 14
- Use uma integral tripla para calcular o volume do sólido limitado por:
-
, , , , no primeiro octante.
Ver solução completaQuestão 15
Determine o volume do sólido formado pela esfera centrada na origem de raio com o cilindro de equação com um número real maior que zero.
Ver solução completaQuestão 18
- Considere a integral iterada
- Expresse em coordenadas cilíndricas e calcule o seu valor.
Questão 19
Seja o volume do sólido comum às esferas e . Expresse (sem calcular) o volume de em coordenadas cilíndricas na ordem .
Ver solução completaQuestão 21
- Calcule a massa do sólido , limitado pelas superfícies , e , se a densidade é dada por .
Ver solução completaQuestão 22
Considere o cone .
b) Usando obrigatoriamente uma integral tripla, calcule o volume do sólido que se encontra no primeiro octante e é limitado pela superfície e o plano .
Ver solução completaQuestão 23
Use integração tripla em coordenadas cilíndricas para calcular o volume do sólido delimitado pelas superfícies e .
Ver solução completaQuestão 24
Usando uma integral tripla, calcule o volume do sólido delimitado pelas superfícies e .
Ver solução completaQuestão 25
Calcule
Onde é a região do espaço limitada lateralmente pelo cilindro , superiormente pelo plano e inferiormente pelo paraboloide
Ver solução completaQuestão 26
A seção reta do interior de uma taça é descrita pela equação , onde corresponde ao fundo da taça e à sua altura
Note: Como a taça tem simetria axial, usamos coordenadas cilíndricas!
(a) Esboce a seção reta e determine sua área;
(b) Determine o volume contido na taça.
Ver solução completaQuestão 27
Seja a seguinte região de delimitada pela superfície de equação , o gráfico da função e o plano .
- Esboce a região
- Calcule o volume da região
Questão 28
Calcule onde é a região de interna ao cilindro , externa ao cilindro , limitada acima pelo semicone e abaixo pelo paraboloide .
a)
b)
c)
d)
e)
Ver solução completaQuestão 35
Questão 2: Usando coordenadas cilíndricas calcule
Onde é a região situada acima do plano , e abaixo do cone
Ver solução completaQuestão 36
3) Arraste e solte, nos campos correspondentes, o valor correto de cada elemento, conforme as opções disponíveis.
b) onde:
e
Ver solução completaQuestão 37
Considere o sólido delimitado pelo cilindo e pelos planos e . Sabendo que a densidade em um ponto de é igual à distância do ponto até o eixo , determine a massa de .
Ver solução completaQuestão 38
Converta a integral abaixo para uma integral equivalente em coordenadas cilíndricas e calcule o resultado.
Ver solução completaQuestão 40
Seja o sólido determinado pelas determinado pelas desigualdades uma unção contínua em e Considere as seguintes afirmações
A(s) afirmação(ões) verdadeira(s) para toda função como acima é(são):
Ver solução completaQuestão 41
Seja .
Considere a região compacta do espaço, onde .
Considere a integral tripla:
- Expresse na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas (Neste item não é pedido o cálculo da integral).
- Calcule , em termos de .
- Seja . E, seja:
- Esboçe .
- Encontre o número real , tal que .
Questão 42
Considere as constantes positivas e com e:
Seja a integral tripla
a) Para esboce o desenho de . Escreva na forma de uma integral iterada, usando obrigatoriamente coordenadas cilíndricas . Não é necessário calcular a integral!
b) Para , calcule em função de .
Ver solução completaQuestão 43
Seja
- Represente graficamente o conjunto
- Usando coordenadas cilíndricas, calcule
Questão 44
Considere o campo e seja a superfície do cone dado por com .
Calcule o volume do cone sólido dado por
Usando a integral tripla.
Ver solução completaQuestão 45
3. Considere o sólido delimitado pelo paraboloide e o plano .
- Esboce
- Calcule o volume de .
Questão 47
Sabendo que a densidade em qualquer ponto é proporcional à distância do ponto ao eixo z,
determine a massa do sólido cortado do cilindro espesso pelo cone e delimitado inferiormente por .
Ver solução completaQuestão 48
(Capítulo 15.8 – Exercício 18)
Utilize coordenadas cilíndricas
Calcule , onde é limitado pelo paraboloide e o plano .
Ver solução completaQuestão 49
(Capítulo 15.7 – Exercício 20) Use a integral tripla para determinar o volume do sólido dado.
O sólido limitado pelos paraboloides e
Ver solução completaQuestão 50
(Capítulo 15.8 – Exercício 20) Utilize coordenadas cilíndricas.
Calcule , onde está delimitado pelos planos e e pelos cilindros e .
Ver solução completaQuestão 51
(Capítulo 15.8 – Exercício 30) Calcule a integral, transformando para coordenadas cilíndricas.
Ver solução completaQuestão 52
(Capítulo 15.7 – Exercício 23)
a) Expresse o volume da cunha no primeiro octante que é cortada do cilindro pelos planos e como uma integral tripla.
b) Utilize a Tabela de Integrais (nas Páginas de Refêrencia 6-10) ou sistema de computação algébrica para determinar o valor exato da integral tripla da parte (a).
Ver solução completaQuestão 53
Calcule a integral tripla.
Onde é limitado pelo cilindro e pelos planos , e no primeiro octante.
Ver solução completaQuestão 54
(Capítulo 15.8 – Exercício 19) Utilize coordenadas cilíndricas
Calcule , onde é o sólido do primeiro octante que está abaixo do paraboloide .
Ver solução completaQuestão 55
Calcule a integral tripla.
Onde é delimitado pelo cilindro parabólico e e pelos planos e
Ver solução completaQuestão 56
(Capítulo 15.7 – Exercício 22) Use a integral tripla para determinar o volume do sólido dado.
O sólido limitado pelo cilindro e pelos planos e
Ver solução completaQuestão 57
8) A integral tripla
fornece o volume do sólido , onde
- é o sólido limitado pelo plano e pelas superfícies e .
- é o sólido limitado pelo plano e pelas superfícies e
- é o sólido limitado pelo plano e pela superfície .
- é o sólido limitado pelo plano e pelas superfícies e .
- é o sólido limitado pelo plano e pelas superfícies e .
Questão 60
Encontre a massa da região sólida limitada pelas superfícies e se a densidade do sólido é .
Ver solução completaQuestão 61
Questão 4: Determine o volume do sólido limitado superiormente pelo plano , inferiormente pelo plano e lateralmente pelo cilindro .
Ver solução completaQuestão 63
Seja o sólido que resulta da interseção das regiões , , , e , calcular o volume de .
Ver solução completaQuestão 64
Calcule o volume do sólido , sabendo que é a região contida em cujos pontos satisfazem e , sendo uma constante maior que zero.
Ver solução completaQuestão 65
Encontre o volume da região sólida limitada abaixo pelo plano , lateralmente pelo cilindro e acima pelo paraboloide .
Ver solução completaQuestão 66
Usando uma integral tripla, calcule o volume do sólido delimitado pelas superfícies e .
Ver solução completaQuestão 67
Usando uma integral tripla, calcule o volume do sólido delimitado pelas superfícies e .
Ver solução completaQuestão 68
Calcule o volume do sólido que está acima do cone e abaixo da esfera .
Ver solução completaQuestão 69
Sejam as superfícies dadas pelas equações implícitas
e seja a região limitada pelas superfícies e que contém a origem.
a) Faça o esboço da região
b) Calculea seguinte integral tripla:
Ver solução completaQuestão 71
Calcule a integral
onde é a região entre os cilindros e limitada pelos planos e por
Ver solução completaQuestão 72
Utilize as coordenadas esféricas
e calcule as integrais dadas a seguir, utilizando a formula da mudança de variáveis:
Onde }
onde R é a região contida dentro do cilindro e , entre os planos z=0 até z=x+y+3
Ver solução completaQuestão 73
Utilize as coordenadas cilíndricas
e calcule as integrais dadas a seguir, utilizando a formula da mudança de variáveis:
Onde
onde R é a região contida dentro do cilindro entre os planos z=-5 até z=4
Ver solução completaQuestão 75
Calcule o valor da integral tripla , em que está acima do plano , abaixo do plano e dentro do cilindro , conforme mostra a figura abaixo.
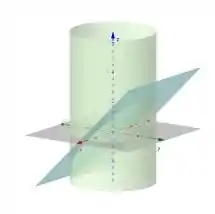
Questão 77
Use a integral tripla para encontrar o volume dentro de acima de e abaixo de .
Ver solução completaQuestão 79
Considere o sólido que está dentro da esfera , acima do plano e abaixo do cone . Calcule o volume de utilizando coordenadas:
(a) Cilíndricas.
Ver solução completaQuestão 80
Utilize as coordenadas cilíndricas
e calcule as integrais dadas a seguir, utilizando a formula da mudança de variáveis:
Onde
onde R é a região contida dentro do cilindro e , entre os planos z=0 até z=x+y+3
Ver solução completaQuestão 81
Utilize as coordenadas cilíndricas
e calcule as integrais dadas a seguir, utilizando a formula da mudança de variáveis:
Onde
onde R é a região contida dentro do cilindro e , entre os planos z=0 até z=x+y+3
Ver solução completaQuestão 82
Questão 2:
Seja a região de no quadrante , , entre as superfícies cujas equações implícitas são , , e abaixo da superfície cuja equação implícita é .
- Faça um esboço de .
- Calcule o volume de .
- Seja a região de que é a união de e a reflexão de no plano , ou seja: é a região acima da superfície , abaixo das superfícies e , e entre as superfície e . Calcule a integral tripla:
Questão 83
- Use uma integral tripla para calcular o volume do sólido limitado por:
-
e , situado no interior do cilindro , .
Ver solução completaQuestão 84
Seja a região do espaço definida pelas desigualdades:
(b) Escreva
Como uma integral repetida (iterada), sem contudo efetuar os cálculos, usando coordenadas cilíndricas
Ver solução completaQuestão 86
Calcule a integral
Onde é o sólido que está dentro do cilindro , o plano , e abaixo do cone
Ver solução completaQuestão 90
Calcule as seguintes integrais:
c) , onde é o sólido limitado pelo cilindro , pelo cone e contido no semiespaço .
Ver solução completa