Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 7
Identifique a superfície de acordo com a equação dada.
Passo 1
E aí, meus amigos! Tudo na paz?
Nesse exercício iremos analisar a equação:
Para identificar a superfície que a equação está descrevendo. Para isso vamos pensar no sistema de coordenas cilíndricas , e e nas suas equações.
Como o enunciado nos dá a equação em função de , vamos usar a equação do sistema de coordenadas cilíndricas:
Nesse sistema também temos para e :
Daí vamos manipular essa equação do enunciado até acharmos a superfície.
Certo? Então, bora lá!
Passo 2
Como temos, da transformação para coordenadas cilíndricas, que:
Então, substituindo esse valor na equação dada no enunciado, temos:
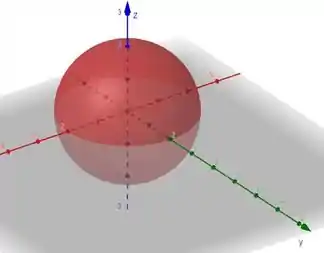
Essa é a equação de uma esfera com raio 2 e centro na origem. A imagem a seguir ilustra a superfície:
Resposta
Essa é a equação de uma esfera com raio 2 e centro na origem.