Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 10

Estabeleça uma propriedade geométrica comum a todas as retas da família e esboce cinco dessas retas.

(a) a família y = b

(b) a família A x + 2 y + 1 = 0

(c) a família 2 x + B y + 1 = 0

(d) a família y - 1 = m ( x + 1 )

Passo 1

Antes, vamos ver como é construída a equação de uma reta. A equação da família das retas é desse tipo:

y = m x + b

Onde m é a inclinação (coeficiente angular) e b é o coeficiente linear (onde corta o eixo y ).

Agora, vamos analisar cada uma das famílias em relação aos coeficientes delas, ok?

Passo 2

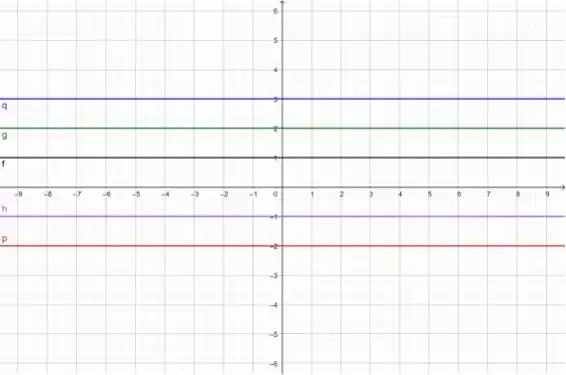
(a) a família y = b

Bem, olhando para a equação dessa família, vemos que m = 0 . Logo, todas as retas dessa família possuem o coeficiente angular sendo 0 . Qual vai ser a cara delas? Bom, tendo o coeficiente angular sendo 0 , nós teremos uma reta constante, cujo valor da constante será ditado por b . Vamos ver.

Passo 3

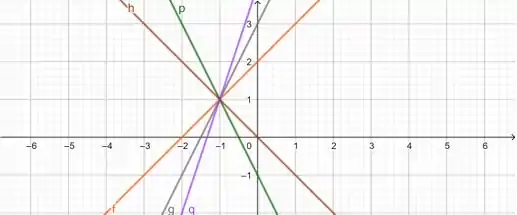
Esboçando 5 dessas retas:

f ( x ) = 1 ;

g ( x ) = 2 ;

h ( x ) = - 1 ;

p ( x ) = - 2 ;

q x = 3 ;

Passo 4

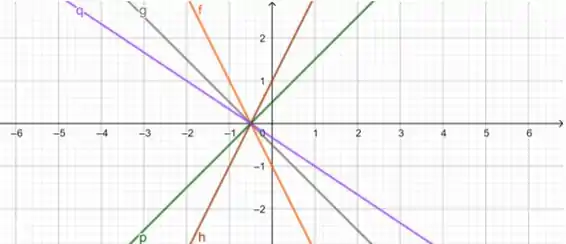
(b) a família A x + 2 y + 1 = 0

Vamos arrumar essa equação antes:

2 y = - 1 - A x

∴

y = - 1 2 - A 2 x

Bem, olhando para a equação dessa família, vemos que b = - 1 2 . Logo, todas as retas dessa família possuem o coeficiente linear sendo - 1 2 , ou seja, as retas cortam o eixo y em y = - 1 2 .

Passo 5

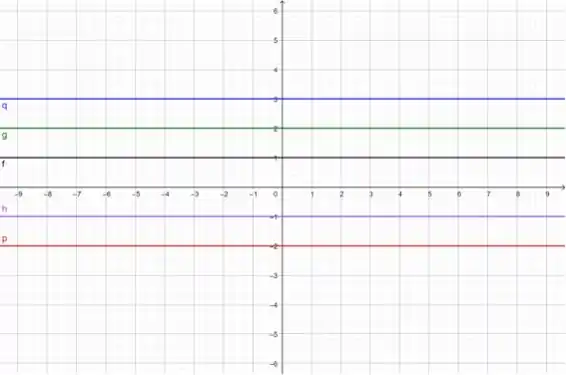
Esboçando 5 dessas retas:

A = 1 → f x = - 1 2 x - 1 2 ;

A = 2 → g x = - x - 1 2 ;

A = - 1 → h ( x ) = 1 2 x - 1 2 ;

A = - 2 → p ( x ) = x - 1 2 ;

A = 0 → q x = - 1 2 ;

Passo 6

(c) a família 2 x + B y + 1 = 0

Arrumando essa equação:

B y = - 2 x - 1

∴

y = - 2 B x - 1 B

Bem, olhando para a equação dessa família, vemos que b = - 1 B . Logo, todas as retas dessa família possuem o coeficiente linear sendo - 1 / B   , ou seja, as retas cortam o eixo y em y = - 1 / B .

Além disso, temos que o coeficiente angular também será dado pelo valor de B , já que ele vale - 2 / B . Mas, como B aparece no denominador, não podemos ter B = 0 , pois teríamos uma divisão por 0 .

Passo 7

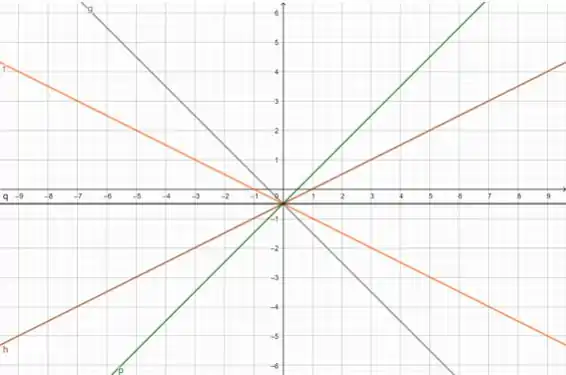
Esboçando 5 dessas retas:

B = 1 → f x = - 2 x - 1 ;

B = 2 → g x = - x - 1 2 ;

B = - 1 → h x = 2 x + 1 ;

B = - 2 → p x = x + 1 2 ;

B = 3 → q x = - 2 3 x - 1 3 ;

Passo 8

(d) a família y - 1 = m ( x + 1 )

Arrumando essa equação:

y - 1 = m x + m

∴

y = m x + ( m + 1 )

Bem, olhando para a equação dessa família, vemos que b = m + 1 . Logo, todas as retas dessa família possuem o coeficiente linear sendo m + 1 , ou seja, as retas cortam o eixo y em y = m + 1 .

Alpem disso, vemos que m = m . Logo, todas as retas dessa família possuem o coeficiente angular sendo m .

Passo 9

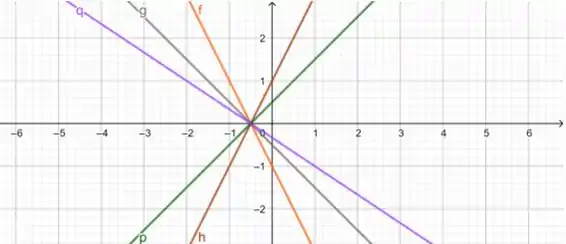
Esboçando 5 dessas retas:

m = 1 → f x = x + 2 ;

m = 2 → g x = 2 x + 3 ;

m = - 1 → h x = - x ;

m = - 2 → p x = - 2 x - 1 ;

m = 3 → q x = 3 x + 4 ;

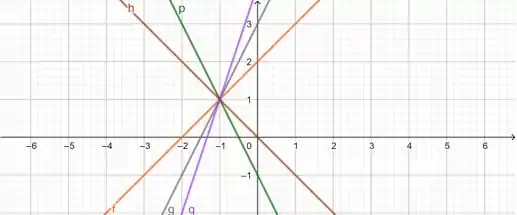
Resposta

(a)

(b)

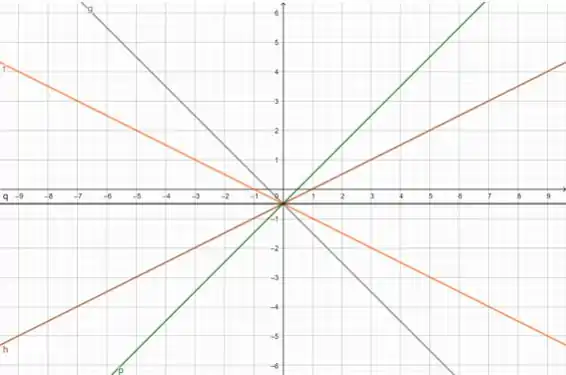
(c)

(d)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dê o domínio e esboce o gráfico.s ) y = sqrt(x + 2)
Dê o domínio e esboce o gráfico.n ) y = (1)/(( x + 1 )^2)
Dê o domínio e esboce o gráfico.o ) y = 1 + (1)/(x^2)
Dê o domínio e esboce o gráfico.l ) f (x) = (1)/(( x - 1 )^2)
Dê o domínio e esboce o gráfico.t ) y = root(3)(x)