Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 15t
Dê o domínio e esboce o gráfico.
Passo 1
Essa função é do tipo racional do tipo:
Como o índice é ímpar, pode assumir qualquer valor, então seu domínio é dado por:
No nosso caso , então o domínio pode ser escrito como:
Passo 2
Vamos ver alguns pontos que satisfazem essa função. Começando pela raiz da função:
Então nossa função passa pela origem das coordenadas: .
Para : , então .
Para , então .
Passo 3
Vamos agora ao esboço:
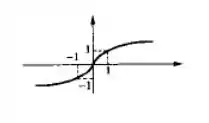
Resposta
Exercícios de Livros Relacionados
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f + g f x = x - 5 ; g x = x 2 - 1
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f ∙ g f x = x 2; g x = 1 x
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f - g f x = x 2 + 1; g x = 3 x - 2
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f / g f x = x + 1 x - 1 ; g x = 1 x
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f / g f x = | x |; g x = | x - 3 |