Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.1 - Ex. 3a
Estime a área sob o gráfico de de até usando quatro retângulos aproximantes e extremos direitos. Esboce o gráfico e os retângulos. Sua estimativa é uma subestimativa ou uma superestimativa?
Passo 1
Vamos dividir o intervalo de entre 1 e 5 em quatro partes, cada parte de tamanho 1. Então, no gráfico de vamos fazer 4 retângulos para aproximar a área, cada retângulo tendo como base um intervalo de tamanho 1 e como altura a função no extremo direito do intervalo. Somando as áreas dos quatro retângulos, teremos a nossa área abaixo da curva aproximada.
Passo 2
Primeiro vamos esboçar a curva , para o intervalo de a :
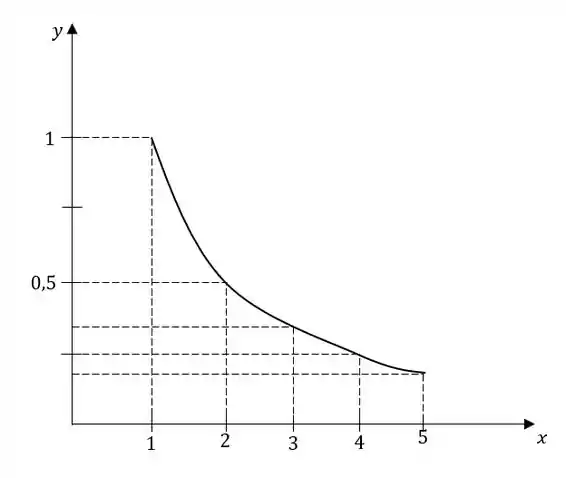
Agora, para desenhar os retângulos, tomamos como altura a função do lado direito de cada intervalo de tamanho 1:
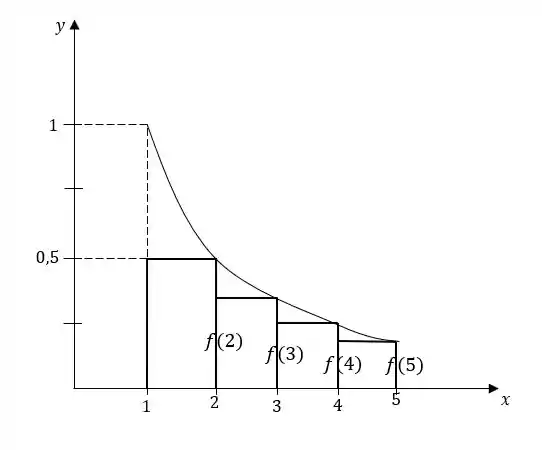
Passo 3
Então fazemos o cálculo da soma das áreas dos retângulos:
Pela figura, podemos ver que a área real sob a curva é maior qe a que calculamos, então nosso resultado é uma subestimativa.