Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 45

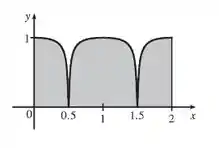
Esboce o gráfico de uma função contínua no intervalo 0,2 para a qual a Regra do Trapézio, com n = 2 , seja mais apropriada que a Regra do Ponto Médio.

Passo 1

Vamos considerar um função f do gráfico abaixo:

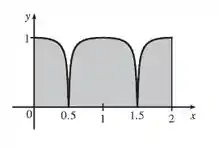
A área ∫ 0 2 f x d x se aproxima de 2 . Pela Regra do Trapézio nós temos:

O intervalo 0 ≤ x ≤ 2 , e vamos usar n = 2 , temos que ∆ x :

∆ x = b - a n = 2 - 0 2 = 1

Para achar a aproximação pela Regra do Trapézio fazemos uma média das aproximações da soma de Riemann, com a fórmula:

T n = 1 2 ∆ x f x 0 + 2 f x 1 + 2 f x 2 + ∙ ∙ ∙ + 2 f x n - 1 + f x n

T 2 = 1 2 ∆ x f 0 + 2 f 1 + 2 f 2 = 1 2 ∙ 1 1 + 2.1 + 1 = 2

Passo 2

Agora vamos achar a aproximação do ponto médio M 2 , onde os x dos pontos são os pontos médios de cada intervalo:

M n = ∑ i = 1 n f x i - ∆ x = f x - 1 + f x - 2 + f x - 3 ∙ ∙ ∙ + f x - n ∆ x

M 2 = ∑ i = 1 n f x i - ∆ x = f 0,5 + f 1,5 1 = 0 + 0 = 0

Assim, a Regra do Trapézio é mais apropriada.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A intensidade de luz com comprimento de onde λ viajando através de uma grade de difração com N fendas a um ângulo θ é dada por I θ = N 2 sen 2 ⁡ k k 2 , em que k = π N d sen ⁡ θ λ e d é a distância en
Mostre que 1 2 T n + M n = T 2 n .
A tabela mostra os valores de uma função força f x onde x é medido em metros e f x , em newtons. Use a Regra de Simpson para estimar o trabalho realizado por essa força para mover um objeto por uma di
Use a Regra do Trapézio com n = 10 para aproximar ∫ 0 20 cos ⁡ π x d x . Compare seu resultado com o valor real. Você pode explicar a discrepância?
Mostre que se f for um polinômio de grau três ou menor, então a Regra de Simpson dá o valor exato de ∫ a b f x d x .