Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 40

A tabela mostra os valores de uma função força f x onde x é medido em metros e f x , em newtons. Use a Regra de Simpson para estimar o trabalho realizado por essa força para mover um objeto por uma distância de 18 m.

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente estimar o trabalho realizado por uma força para mover um objeto por uma distância de 18   m . Pra isso, ele nos deu a tabela de correlação entre a força f ( x ) e a distância x , medida em metros.

Olhando a tabela, gente percebe que o intervalo considerado vai de zero até 18 metros, ou seja:

0 ≤ x ≤ 18

Além disso, após x = 0 , temos 6 medições de força. Então, teremos n = 6 e a variação das medições será dada por:

Δ x = b - a n

Onde a e b são extremos do intervalo [ 0 ,   6 ] . Depois disso, basta a gente aplicar a fórmula de Simpson:

S n = f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + ∙ ∙ ∙ + 2 f x n - 2 + 4 f x n - 1 + f x n ∆ x 3

Considerando que S n seja o trabalho realizado e f x n as medições de força oferecidas pela tabela.

Vamos lá!

Passo 2

Temos o intervalo 0 ≤ x ≤ 18 , e vamos usar n = 6 , temos que ∆ x :

∆ x = b - a n = 18 - 0 6 = 3

Agora vamos olhar na tabela para extrair os valores da função no intervalo:

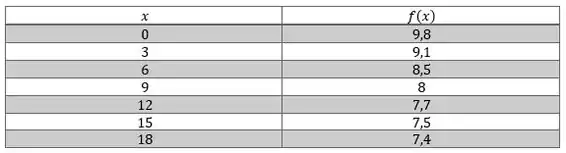
Com a Regra de Simpson é usado parábolas ao invés de segmentos de reta para aproximar a curva, assim a fórmula fica com um padrão 1 , 4 , 2 , 4 , 2 , . . . , 4 , 2 , 4 , 1 :

S n = ∆ x 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + ∙ ∙ ∙ + 2 f x n - 2 + 4 f x n - 1 + f x n

Substituindo os valores da tabela:

S 6 = Δ x 3 f 0 + 4 f 3 + 2 f 6 + 4 f 9 + 2 f 12 + 4 f 15 + f 18

S 6 = 1 3 . 3 9,8 + 4 ∙ 9,1 + 2 ∙ 8,5 + 4 ∙ 8,0 + 2 ∙ 7,7 + 4 ∙ 7,5 + 7,4

E calculando, temos:

S 6 = 148

Portanto, o trabalho estimado realizado por essa força para mover um objeto por uma distância de 18   m é de 148   J .

Valeu, galera! Até a próxima! 😉

Resposta

148   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse o limite como uma integral definida no intervalo dado. lim n → ∞ ⁡ ∑ i = 1 n x i ln ⁡ 1 + x i 2 ∆ x ,2,6
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ - 1 5 1 + 3 x d x
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ 1 2 x 3 d x
As massas pontuais m i estão localizadas no eixo x conforme mostra a figura a seguir. Ache o momento M do sistema com relação à origem e o centro de massa x - .
Depois de uma injeção de 8m g de contraste, as leituras de concentração do contraste, em m g / L , a intervalos de dois segundos, são mostradas na tabela. Use a Regra de Simpson para estimar a capacid