Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 63

Estime os intervalos da concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de f ' .

f x = x 4 + x 3 + 1 x 2 + x + 1

Passo 1

Fala aí! tudo certinho?

Nesse problema foi dada a função

f x = x 4 + x 3 + 1 x 2 + x + 1

E nosso objetivo é determinar os intervalos de concavidade de f usando uma ferramenta algébrica e plotar o gráfico de f ' usando uma ferramenta gráfica.

Parece complicado?

Para responder essa questão podemos calcular as derivada de primeira e segunda ordem de f e usando uma ferramenta gráfica, plotar ambos os gráficos...

O gráfico de f ' é pedido no problema, mas o gráfico de f ' ' nos dá os intervalos de concavidade e tambem os pontos de inflexão...

Quando f ' ' > 0 , a concavidade de f é voltada para cima e quando f ' ' < 0 , a concavidade de f é voltada para baixo. Quando f ' ' = 0 temos um ponto de inflexão.

Sacou? Bora começar!

Passo 2

Vamos começar calculando a derivada de primeira ordem...

Pra isso vamos usar a regra do quociente e a regra da cadeia...

f x = x 4 + x 3 + 1 x 2 + x + 1 → f ' x = d x 4 + x 3 + 1 d x · x 2 + x + 1 - x 4 + x 3 + 1 · d x 2 + x + 1 d x x 2 + x + 1 2

f ' x = d x 4 + x 3 + 1 d x · x 2 + x + 1 - x 4 + x 3 + 1 · d x 2 + x + 1 d x · d u d u x 2 + x + 1 2

Resolvendo as derivadas e simplificando o denominador

f ' x = 4 x 3 + 3 x 2 · x 2 + x + 1 - x 4 + x 3 + 1 · 2 x + 1 · 1 2 u x 2 + x + 1

f ' x = 4 x 3 + 3 x 2 · x 2 + x + 1 - x 4 + x 3 + 1 · 2 x + 1 2 x 2 + x + 1 x 2 + x + 1

f ' x = 4 x 3 + 3 x 2 · x 2 + x + 1 · 2 x 2 + x + 1 - x 4 + x 3 + 1 · 2 x + 1 x 2 + x + 1 2 x 2 + x + 1

Perceba que podemos simplificar a raiz do numerador pois o termo x 2 + x + 1 aparece multiplicando ele mesmo

f ' x = 2 4 x 3 + 3 x 2 · x 2 + x + 1 - x 4 + x 3 + 1 · 2 x + 1 x 2 + x + 1 2 x 2 + x + 1

f ' x = 6 x 5 + 11 x 4 + 13 x 3 + 6 x 2 - 2 x - 1 x 2 + x + 1 2 x 2 + x + 1

Aproveitando para plotar o gráfico de f ' , temos

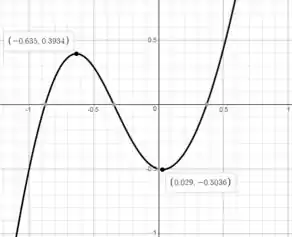
Tranquilo até aqui?

Passo 3

Vamos obter a seguda deriada de f derivando f ' usando tudo que temos direito... rs (temos que usar a regra do quociente, a regra do produto e a regra da cadeia...👀)

f ' ' x = d 6 x 5 + 11 x 4 + 13 x 3 + 6 x 2 - 2 x - 1 d x · x 2 + x + 1 2 x 2 + x + 1 - 6 x 5 + 11 x 4 + 13 x 3 + 6 x 2 - 2 x - 1 · d x 2 + x + 1 2 x 2 + x + 1 d x x 2 + x + 1 2 x 2 + x + 1 2

Como a equação ficou muito grande, vamos por partes...

Começando pelo mais simples, temos

d 6 x 5 + 11 x 4 + 13 x 3 + 6 x 2 - 2 x - 1 d x = 30 x 4 + 44 x 3 + 39 x 2 + 12 x - 2

Agora aplicando a regra do produto...

d x 2 + x + 1 2 x 2 + x + 1 d x = 2 d x 2 + x + 1 d x · x 2 + x + 1 + x 2 + x + 1 · d x 2 + x + 1 d x

Sabemos que a derivada de x 2 + x + 1 é 2 x + 1 2 x 2 + x + 1 pois calculamos isso no passo anterior...

d x 2 + x + 1 d x = 2 x + 1

Substituindo em f ' ' , temos

f ' ' x = 30 x 4 + 44 x 3 + 39 x 2 + 12 x - 2 · x 2 + x + 1 2 x 2 + x + 1 - 6 x 5 + 11 x 4 + 13 x 3 + 6 x 2 - 2 x - 1 · 2 2 x + 1 · x 2 + x + 1 + x 2 + x + 1 · 2 x + 1 2 x 2 + x + 1 x 2 + x + 1 2 x 2 + x + 1 2

Fazendo todas as manipulações possíveis para simplificar f ' ' , vamos chegar em

f ' ' x = 24 x 6 + 64 x 5 + 115 x 4 + 115 x 3 + 92 x 2 + 32 x - 1 4 x 2 + x + 1 5 2

Show?

Passo 4

Vamos plotar o gráfico de f ' ' para verificar seu sinal e a concavidade de f ...

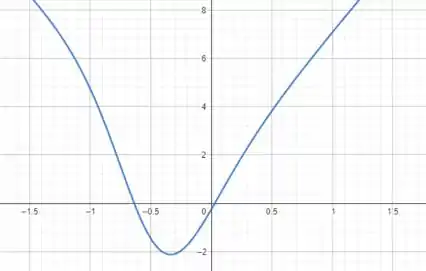
Perceba que f ' ' é positiva até x = - 0,6 e depois de x = 0 e dentro desse intervalo a função f ' ' é negativa.

Como f ' ' está diretamente relacionada com a concavidade de f , podemos afirmar que em - ∞ < x < - 0,6 e em 0 < x < ∞ a função possui concavidade para cima. E quando - 0,6 < x < 0 a função f possui concavidade para baixo.

E fim! O que achou? Entendeu tudo? Responde Aí!

Resposta

f possui concavidade voltada para cima para valores de x aproximadamente nos intervalos ( - ∞   , - 0.6 ) e 0   ,   ∞ e concavidade para baixo no intervalo - 0.6   ,   0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estima-se que um operário de uma oficina que fabrica molduras para quadros possa pintar y molduras, x horas após ter começado a trabalhar às 8 da manhã, e y = 3 x + 8 x ² - x 3 0 ≥ x ≤ 4 ² Ache o mome
Se f x = x 5 , mostre que 0 é um número crítico de f , mas que f ( 0 ) não é um extremo relativo. A origem é um ponto de inflexão do gráfico de f ? Prove sua resposta,
Encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico e mostre um segmento da
Encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico e mostre um segmento da
Encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico e mostre um segmento da