Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 58
Use os métodos desta seção para esboçar a curva , onde a é uma constante positiva. O que os membros desta família têm em comum? Como eles diferem entre si?
Passo 1
Fala meus queridões. Nessa questão nós temos uma família de funções dada por:
Onde é uma constante positiva, dessa forma, vamos avaliar o comportamento do gráfico dessa família de funções aplicando os testes que temos.
Começando pelas assíntotas horizontais.
Quando vai para o infinito:
Para encontrar o resultado dessa indeterminação, colocamos o em evidência:
A divisão por infinito resulta em zero, logo:
Portanto,
E quando vai para o infinito negativo, temos:
Portanto,
Passo 2
Se
Então a derivada é:
E a derivada segunda é:
Temos que a função é crescente quando e decrescente quando .
Para crescente:
ou
Para decrescente:
Então é crescente para valores de nos intervalos e e decrescente em .
No ponto em que a função passa de crescente para decrescente temos uma máximo local e no ponto em que a função passa de decrescente para crescente temos um mínimo local.
Sendo assim temos máximo local no ponto e mínimo local no ponto .
A função possui concavidade para cima quando e possui concavidade para baixo quando .
Dessa forma,
Para com concavidade para cima:
Para com concavidade para baixo:
Logo, possui concavidade para baixo em valores de no intervalo e concavidade para cima em . O pondo de inflexão é o ponto onde a função troca de concavidade que nesse caso é .
Passo 3
Com essas informações que são:
A função cresce para ou para e decresce entre .
A função possi máximo em e mínimo em .
A função é côncava para cima em e côncava para baixo em .
O ponto de inflexão é em .
Temos o esboço:
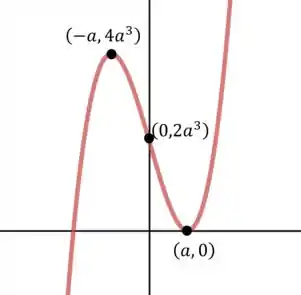
A diverença entre os membros da família está nos pontos de máximo, mínimo e de inflexão que são dados por .
Resposta
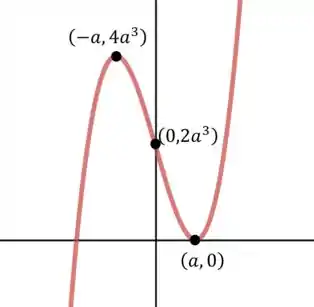
A diverença entre os membros da família está nos pontos de máximo, mínimo e de inflexão que são dados por .