Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 22
22. Faça uma conjectura sobre o valor do limite (se ele existir) por meio dos valores da função nos números dados (com precisão de seis casas decimais).
Passo 1
Belezoca de motoca galera!
Nesse problema foi dado o limite
E nosso objetivo é determinar seu resultado a partir de uma tabela para determinados valores de .
Parece complicado?
Para resolver esse problema, vamos usar uma calculadora e construir uma tabela para cada valor de .
Assim podemos estimar um valor para o limite.
Veja só!
Passo 2
Vamos montar então uma tabela com os respectivos valores da função para cada .
Por exemplo para , temos que
Construindo uma tabela com todos os valores de dados e os respectivos ficamos com
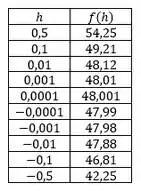
E já que queremos o limite quando tende a , quer dizer que nosso valor deve estar entre os valores de e
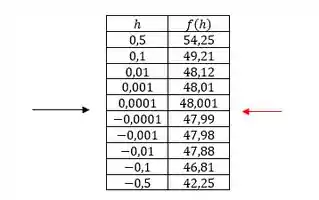
Dessa forma, podemos concluir que o limite tende a 48, portanto
E aí! entendeu tudo? Responde Aí!