Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 23
Use uma tabela de valores para estimar o valor do limite. Caso tenha um dispositivo de gráficos, usar para confirmar o resultado.
Passo 1
Fala aí, galerinha! 😉
Nesse problema queremos obter o limite
E pra isso foi pedido para usarmos o método da tabela de valores.
Tem ideia de como fazemos isso? 😉
Este método consiste em substituir os valores de tanto pela esquerda (valores menores que ) quanto pela direita (valores maiores que ) de modo que seja possivel observar uma convergência de valores pelos dois lados...
Se essa convergência não acontecer, significa que o limite não existe...
Veja só! 😬
Passo 2
Bom pessoal, para existir o limite, a função deve tender a um certo valor tanto pela esquerda quanto pela direita.
Vamos então usar a calculadora com valores próximos ao limite, pela esquerda e pela direita, para confirmar ou não essa tendência.
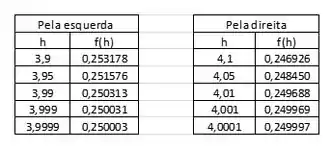
Vemos então que a tendência do limite é igual a já que quanto mais nos aproximamos de , mais próximo de a função está.
Confirmando no gráfico:
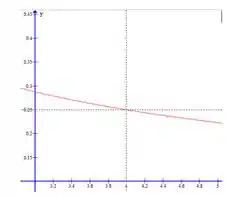
Portanto, o limite:
E aí! entendeu tudo? Responde Aí! 😉
