Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 21
Estime o valor do limite (se existir) pela avaliação da função nos números dados (usar 6 casas decimais).
Passo 1
Olá, meu amigo. Aqui a questão quer que analisemos o limite da função, caso ele exista, por meio do calculo dos valores da função. Então o que iremos fazer é calcular os valores de e analisar se o limite existe ou não e caso exista para onde ele caminha.
Bom pessoal, para existir o limite, a função deve tender a um certo valor tanto pela esquerda quanto pela direita.
Passo 2
Basta então usar a calculadora com os valores dados e ver se esta tendência existe, e qual é.
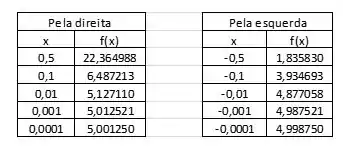
Vemos então que a tendência do limite é igual a
Portanto, o limite:
Resposta
Exercícios de Livros Relacionados
Ache o limite lim t → 0 - 3 + x 2 x
Ache o limite lim x → 3 - x 3 + 9 x 2 + 20 x x 2 + x - 12
Faça o seguinte: a ) Use uma calculadora para tabular valores de f x para valores fixados de x e, a partir deles, faça uma afirmação a respeito do comportamento evidente de f x . b ) Ache o limite ind
Ache o limite lim t → 2 + t + 2 t 2 - 4
Ache o limite lim t → 0 3 + x 2 x 2