Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 2h
Estude o sinal da expressão.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente estudar o sinal da expressão, isso quer dizer que ele quer saber onde essa função é positiva, onde ela é negativa e quais são os zeros (as raízes) da função.
Então, vamos analisar três situações, quando a expressão toda é maior que zero, quando é menor que zero e quando é igual a zero. Pra isso, vamos verificar o sinal do numerador e do denominador separadamente, para que o resultado satisfaça a expressão que desejamos, que, no caso, são:
Para maior do que zero:
Para menor do que zero:
E para igual a zero:
Passo 2
Para estudar o sinal da expressão vamos analisar o numerador e o denimonador separadamente:
Para temos o seguinte esquema:
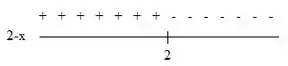
A expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
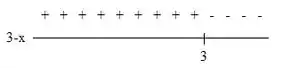
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Beleza, mas o que isso quer dizer? Nossa primeira condição é que , ou seja, o quociente seja positivo. Então, com base nos sinais que vimos nos termos do numerador e denominador, vamos construir nosso quadro de sinais:
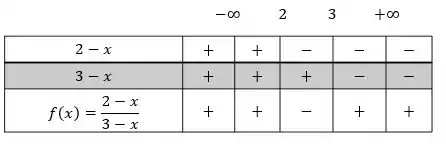
Repare que a nossa função é positiva para e para , ou seja, no intervalo:
Passo 3
A mesma análise que fizemos no passo , serve para verificar o que acontece quando a nossa expressão geral é menor do que zero (negativa). Então, vamos olhar de novo para o quadro de sinais que construímos:
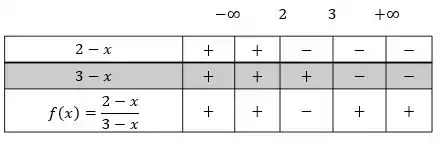
Repare que a nossa função só é negativa (ali na última linha da tabela), quando tá entre e . Isso quer dizer que para , temos:
Ou, na notação de intervalo, .
Passo 4
Agora vamos resolver a equação para quando nossa função é igual a zero:
Como o denominador nunca pode zerar, para que esse quociente seja zero, precisamos que a expressão do numerador seja igual a zero. Assim temos:
Valeu, galera. Até a próxima! 😉
Resposta
para ou
para
para e não está definida para