Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 9.Exercícios - Ex. 208b
Estude a variação das seguintes funções reais: a)
Passo 1
Nosso primeiro passo será reescrever a expressão da nossa função em algo mais fácil de se estudar. Podemos perceber que nossa função é dada pode ser escrita na forma:
Passo 2
Dado o primeiro passo, conseguimos perceber que dentro dos parênteses temos a expressão do , então vamos substituí-la:
Passo 3
Para simplificar ainda mais a nossa função, vamos nos lembrar da fórmula:
Viu que é bem parecido com o que temos na nossa expressão? A única diferença é que na nossa função temos o , então nosso “a” da fórmula seria . Então vamos substituir e ficar com:
Passo 4
Agora podemos estudar nossa função de forma mais eficiente, para isso vamos utilizar uma tabela:
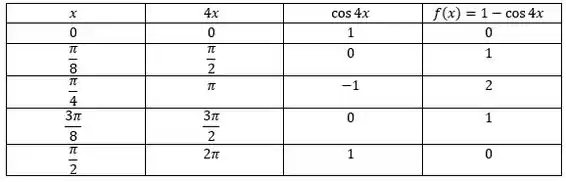
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Prove as identidades:1 - tanh^2 u = sech^2 u ;1 - c o t g h^2 u = - c o s s e c h^2 u .
Construir o gráfico das seguintes funções trigonométricas. Verificar se são periódicas e em caso afirmativo determinar o período. y = sen k x ,k = 2 ,3 , 1 2e 1 3 ; y = k cos x ,k = 2 ,3 , 1 2 , 1
Construir o gráfico das seguintes funções trigonométricas. Verificar se são periódicas e em caso afirmativo determinar o período. y = sen k x ,k = 2 ,3 , 1 2e 1 3 ; y = k cos x ,k = 2 ,3 , 1 2 , 1
Prove as identidades:1 - tanh^2 u = sech^2 u ;1 - c o t g h^2 u = - c o s e c h^2 u .
Mostre a validade das expressões:a r g cosh x = ln ( x + sqrt(x^2 - 1) ) , x = 1 ;arg tanh x = (1)/(2) ln ((1 + x)/(1 - x)) , - 1x1 ;arg sech x = ln ((1 + sqrt(1 - x^2))/(x)) , 0x = 1