Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 34
Se
então a raiz da equação é . Explique por que o método de Newton falha para encontrar a raiz, não importando que aproximação inicial é usada. Ilustre sua explicação com um esboço.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função definida por partes...
E nosso objetivo é mostrar que o método de Newton é incapaz de determinar sua raiz se .
Parece complicado?
Vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula:
Primeiro temos que para e para .
O método consiste em aplicar a fórmula em ciclos até obtermos dois resultados iguais com a precisão desejada.
Porém já sabemos que esse método não funciona para essa função, então vamos aplica-la para ver o que acontece!
Bora lá!
Passo 2
Vamos começar montando nossa fórmula e pra isso vamos derivar em ambas as partes...
Para , temos ... aplicando a regra da potência.
Para , temos , aplicamos a regra da cadeia...
Agora vamos montar duas formulas... uma para e outra para ...
Para , temos
Como ...
Agora para , fazemos a mesma coisa...
Como ...
Tranquilo até aqui?
Passo 3
Dá pra ver que depois de escolher qualquer valor de , os próximos valores vão ficar alternando entre e , nunca chegando a raiz, dá pra ver isso também no gráfico abaixo:
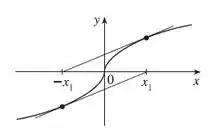
Ou seja, o método de Newton não converge para um valor, logo, ele falha nesse caso.
E aí! o que achou? Responde Aí!
Resposta
Depois de escolher qualquer valor de , os próximos valores vão ficar alternando entre e , nunca chegando a raiz.