Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 42

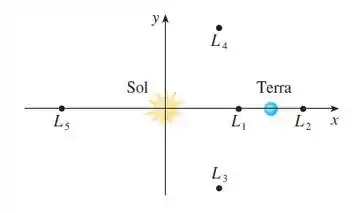
A figura mostra o Sol na origem e a Terra no ponto 1,0 .(A unidade aqui é a distância entre o centro da Terra e o Sol, chamada unidade astronômica: 1 UA ≈ 1,496 × 10 8 km.) Existem cinco localizações L 1 ,   L 2 , L 3 , L 4 e L 5 nesse plano de rotação da Terra em torno do Sol onde um satélite permanece imóvel em relação à Terra, em razão das forças que agem no satélite (inclusive a atração gravitacional da Terra e do Sol) se contrabalancearem. Essas localizações são denominadas pontos de libração. (Um satélite de pesquisa solar foi colocado em um desses pontos.) Se m 1 for a massa do Sol, m 2 for a massa da Terra e r = m 2 m 1 + m 2 , resulta que a coordenada x de L 1 é a única raiz da equação de quinto grau

p x = x 5 - 2 + r x 4 + 1 + 2 r x 3 - 1 - r x 2 + 2 1 - r x + r - 1 = 0

e a coordenada x de L 2 é a raiz da equação

p x - 2 r x 2 = 0

Usando o valor r ≈ 3,04042 × 10 6 , encontre a localização dos pontos de libração (a) L 1 e (b) L 2 .

Passo 1

Fala meus queridos. Nessa questão, nos é dito muita coisa, mas o que queremos de fato é encontrar o valor de x onde:

p x = x 5 - 2 + r x 4 + 1 + 2 r x 3 - 1 - r x 2 + 2 1 - r x + r - 1

p x = 0

E para isso vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula:

x n + 1 = x n - f x n f ' x n

Onde a partir de um chute inicial x 1 podemos encontrar a raíz desse polinômio p x

Vamos agora precisar de p ' x , vamos calcular então:

p ' x = x 5 - 2 + r x 4 + 1 + 2 r x 3 - 1 - r x 2 + 2 1 - r x + r - 1 '

Derivando termo a termo, teremos:

p ' x = 5 x 4 - 4 2 + r x 3 + 3 1 + 2 r x 2 - 2 1 - r x + 2 1 - r

Passo 2

Pronto, agora que temos p ' x é só jogar na fórmula de Newton:

x n + 1 = x n - p x n p ' x n

x n + 1 = x n - x n 5 - 2 + r x n 4 + 1 + 2 r x n 3 - 1 - r x n 2 + 2 1 - r x n + r - 1 5 x n 4 - 4 2 + r x n 3 + 3 1 + 2 r x n 2 - 2 1 - r x n + 2 1 - r

Precisamos agora de um bom chute inicial e do valor de r .

Passo 3

Usando r = 3,04042 × 10 6 e o ponto de libração é um pouco menor que 1 UA, então vamos usar x 1 = 0,95 e vamos substituir na fórmula:

x 2 = x 1 - x 1 5 - 2 + r x 1 4 + 1 + 2 r x 1 3 - 1 - r x 1 2 + 2 1 - r x 1 + r - 1 5 x 1 4 - 4 2 + r x 1 3 + 3 1 + 2 r x 1 2 - 2 1 - r x 1 + 2 1 - r

x 2 = 0,96682

Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de x n deixar de variar, vamos lá:

x 3 = x 2 - x 2 5 - 2 + r x 2 4 + 1 + 2 r x 2 3 - 1 - r x 2 2 + 2 1 - r x 2 + r - 1 5 x 2 4 - 4 2 + r x 2 3 + 3 1 + 2 r x 2 2 - 2 1 - r x 2 + 2 1 - r

x 3 ≈ 0,97770

Mais uma vez, agora com x 4 :

x 4 = x 3 - x 3 5 - 2 + r x 3 4 + 1 + 2 r x 3 3 - 1 - r x 3 2 + 2 1 - r x 3 + r - 1 5 x 3 4 - 4 2 + r x 3 3 + 3 1 + 2 r x 3 2 - 2 1 - r x 3 + 2 1 - r

x 4 ≈ 0,98451

Sucessivamente fazendo vamos achar os valores:

x 5 ≈ 0,98830 ; x 6 ≈ 0,98976 ; x 7 ≈ 0,98998 ; x 8 ≈ 0,98999 e x 9 ≈ 0,98999 .

Assim, L 1 está a 0,98999 UA do sol.

Passo 4

Para a letra b), temos que:

p x - 2 r x 2 = x 5 - 2 + r x 4 + 1 + 2 r x 3 - 1 - r x 2 + 2 1 - r x + r - 1

  p x = x 5 - 2 + r x 4 + 1 + 2 r x 3 - 1 - r x 2 + 2 1 - r x + r - 1 + 2 r x 2

Vamos agora precisar de p ' x , vamos calcular então:

p ' x = x 5 - 2 + r x 4 + 1 + 2 r x 3 - 1 - r x 2 + 2 1 - r x + r - 1 '

Derivando termo a termo, temos:

p ' x = 5 x 4 - 4 2 + r x 3 + 3 1 + 2 r x 2 - 2 1 - r x + 2 1 - r + 4 r x

Passo 5

Pronto, agora que temos p ' x é só jogar na fórmula de Newton:

x n + 1 = x n - p x n p ' x n

x n + 1 = x n - x n 5 - 2 + r x n 4 + 1 + 2 r x n 3 - 1 - r x n 2 + 2 1 - r x n + r - 1 + 2 r x n 2 5 x n 4 - 4 2 + r x n 3 + 3 1 + 2 r x n 2 - 2 1 - r x n + 2 1 - r + 4 r x n

Precisamos agora de r e de um bom chute inicial x 1 .

Passo 6

Usando r = 3,04042 × 10 6 e L 2 é um pouco mais que 1 UA do Sol, e julgando pelo resultado da letra (a), provavelmente menos que 0,02 UA, então vamos usar x 1 = 1,02 e vamos substituir na fórmula:

x 2 = x 1 - x 1 5 - 2 + r x 1 4 + 1 + 2 r x 1 3 - 1 - r x 1 2 + 2 1 - r x 1 + r - 1 + 2 r x 1 2 5 x 1 4 - 4 2 + r x 1 3 + 3 1 + 2 r x 1 2 - 2 1 - r x 1 + 2 1 - r + 4 r x 1

x 2 = 1,01422

Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de x n deixar de variar, vamos lá:

x 3 = x 2 - x 2 5 - 2 + r x 2 4 + 1 + 2 r x 2 3 - 1 - r x 2 2 + 2 1 - r x 2 + r - 1 + 2 r x 2 2 5 x 2 4 - 4 2 + r x 2 3 + 3 1 + 2 r x 2 2 - 2 1 - r x 2 + 2 1 - r + 4 r x 2

x 3 ≈ 1,01118

Mais uma vez, agora com x 4 :

x 4 = x 3 - x 3 5 - 2 + r x 3 4 + 1 + 2 r x 3 3 - 1 - r x 3 2 + 2 1 - r x 3 + r - 1 + 2 r x 3 2 5 x 3 4 - 4 2 + r x 3 3 + 3 1 + 2 r x 3 2 - 2 1 - r x 3 + 2 1 - r + 4 r x 3

x 4 ≈ 1,01018

Sucessivamente fazendo vamos achar os valores:

x 5 ≈ 1,01008 e x 6 ≈ 1,01008

Assim, L 2 está a 1,01008 UA do sol.

Resposta

  1. L 1 = 0,98999 UA
  2. L 2 = 1,01008 UA
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule g^' (x) sendo g dada porg (x) = (1)/(x^3)
Calcule g^' (x) sendo g dada porg (x) = (1)/(x^7)
Calcule g^' (x) sendo g dada porg (x) = root(8)(x)
Calcule g^' (x) sendo g dada porg (x) = x^(- 3)
Calcule g^' (x) sendo g dada porg (x) = x^2