No Exemplo 2 consideramos a função , onde era o índice de sensação térmica ocasionado pelo vento, , a temperatura real e , a velocidade do vento. A representação numérica foi fornecida pela Tabela 1.

(a) Qual o valor de ? Qual seu significado?

(b) Descreva em palavras o significado da questão “Para quais valores de é verdade que ?”. Em seguida, responda à questão.

(c) Descreva o significado da questão “Para quais valores de vale ?”. Em seguida, responda à questão.

(d) Qual o significado da função ? Descreva o comportamento dessa função.

(e) Qual o significado da função ? Descreva o comportamento dessa função.

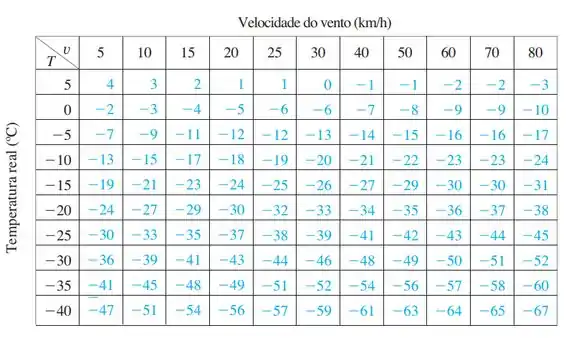
Tabela 1

(a) Observando na tabela, podemos ver que:

Para fazer isso a gente se move na coluna da temperatura e encontra o valor azul na coluna :

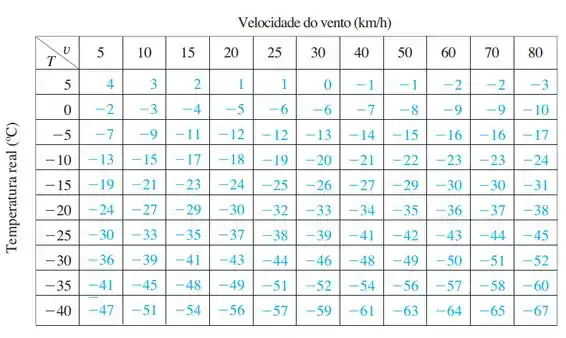
Isso significa que a uma temperatura de com ventos de tem uma sensação térmica é de .

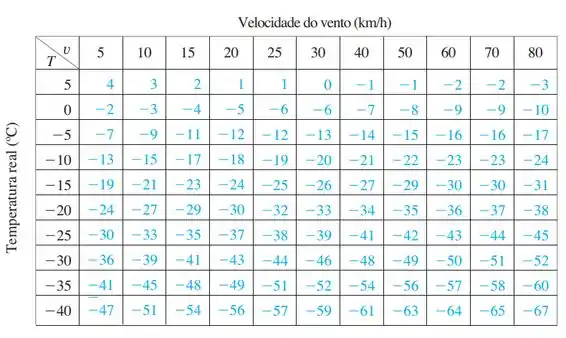
(b) A pergunta busca achar para uma temperatura constante a velocidade do vento para que tenhamos uma sensação de .

Olhando a tabela temos que para a linha onde a velocidade que obedece é

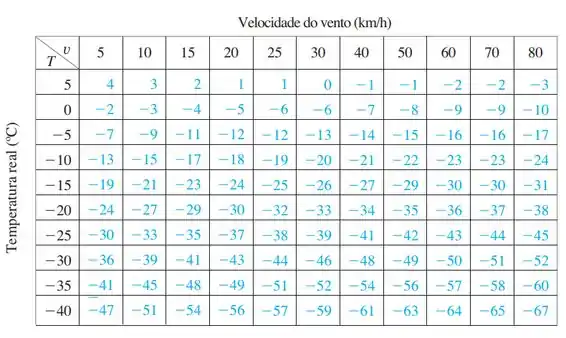
(c) A pergunta busca achar para uma velocidade constante a temperatura para que tenhamos uma sensação de .

Olhando a tabela temos que para a coluna onde a temperatura que obedece é

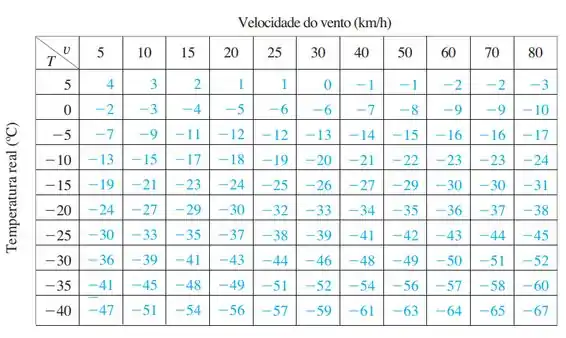
(d) Se olharmos a função , temos uma função de duas variáveis para a sensação térmica, o que significa que a sensação depende de duas variáveis. Se pegarmos , estamos fixando uma das variáveis a um valor constante e então a função agora é de apenas uma variável.

Para descrevermos o seu comportamento, vamo olhar na tabela na linha onde , a sensação está diminuindo, mas nas primeiras colunas a taxa de decremento é maior que no final, então a taxa está aumentando o que resulta em uma relação não linear.

(e) Assim como no item anterior se pegarmos , estamos fixando uma das variáveis a um valor constante e então a função agora é de apenas uma variável.

Para descrevermos o seu comportamento, vamo olhar na tabela na coluna onde , a sensação está diminuindo a uma taxa quase linear.