Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 1c
- Verifique quais dos conjuntos a seguir são abertos em
c)
Passo 1
Graficamente, essa função ficaria,
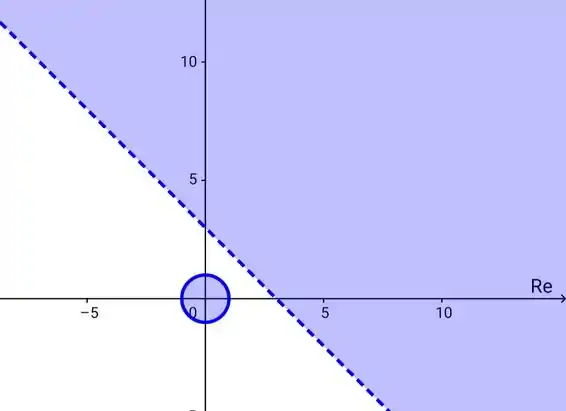
Na expressão temos, graficamente, a linha contínua. Que simboliza que todos os valores menores que o , incluindo o estão dentro do subconjunto. Nesse caso o subconjunto é fechado.
O pontilhado simboliza que todos os valores apenas acima de 3 estão incluídos no conjunto, então nesse caso o intervalo é aberto.
Resposta
O subconjunto é fechado e o aberto.
Exercícios de Livros Relacionados
Sejam F → ,G → ,H → três funções definidas em A ⊂ R e a valores em R 3 . Verifique que F → ⋅ G → + H → = F → ⋅ G → + F → ⋅ H →
Sejam F → t = t , sen t , 2 e G → t = 3 , t , t 2 . Calcule F → t - 2G → t
Sejam F → ,G → ,H → três funções definidas em A ⊂ R e a valores em R 3 . Verifique que F → × G → + H → = F → × G → + F → × H →
Sejam F → ,G → ,H → três funções definidas em A ⊂ R e a valores em R 3 . Verifique que F → × G → = - G → × F →
Represente graficamente e o domínio da função z = f x , y dada por f) z = x - | y |