No Exemplo 1 usamos as equações de Lotka-Volterra para modelar as populações de coelhos e lobos. Vamos modificar aquelas equações como a seguir:
- De acordo com essas equações, o que acontece à população de coelhos na ausência dos lobos?
- Calcule as soluções de equilíbrio e explique seus significados.
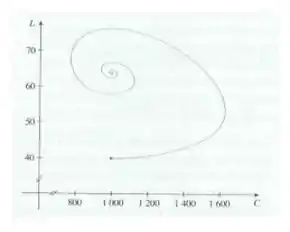
- A figura mostra a trajetória de fase que começa no ponto . Descreva o que acabará ocorrendo com as populações de coelhos e lobos.
- Esboce os gráficos das populações de coelhos e lobos como funções do tempo.
Passo 1
- Queremos analisar as equações dadas e descobrir o que acontece com a população de coelhos quando a população de lobos for igual a .
- Agora precisamos encontrar as soluções de equilíbrio.
- Neste item, nós queremos descrever o que acontecerá com a população de coelhos e lobos ao passar do tempo.
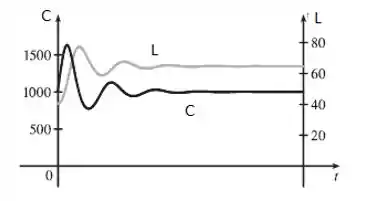
- Agora precisamos desenhar um gráfico que descreva nossa explicação do item (c), assim ficamos com:
Quando , temos
Para que , precisamos que .
Dessa forma, podemos pensar que se , para , nós esperamos que a população de coelhos cresça até , e se , para , podemos esperar que a população de coelhos diminua até . De qualquer forma, ela ficará estável em indivíduos.
Passo 2
Bom, se forem constantes, teremos
Então:
E
Substituindo esses valores na primeira equação, descobrimos que se , então ou
Agora, se , então
Fizemos muitas coisas! Vamos recapitular nossos resultados com calma, temos soluções de equilíbrio:
Caso (i):
Caso (ii): (como calculamos no item (a))
Caso (iii):
Passo 3
Então vamos olhar nosso gráfico:
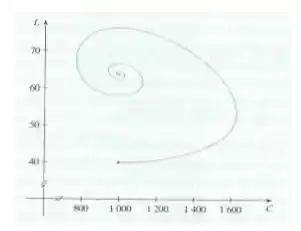
Inicialmente temos lobos e coelhos, ambas as populações vão aumentando, até que a população de coelhos atinge seu máximo em cerca de , então a população de lobos continua a aumentar e a de coelhos começa a diminuir. A população de lobos cresce até atingir seu máximo em (aproximadamente), depois ambas as populações diminuem e começam a oscilar entre diminuírem e aumentarem, até ficarem estáveis em cerca de lobos e coelhos.
Passo 4
Resposta
- Ela ficará estável em indivíduos.
- Caso (i):
Caso (ii): (como calculamos no item (a))
Caso (iii):