Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.6 - Ex. 24

Se, no exercício 22, somente metade da água deve ser bombeada para cima do tanque, ache o trabalho.

Passo 1

Temos no exercício 22 um tanque em forma de cone circular reto invertido de 8 m de diâmetro e com altura de 10m, cheio de água até a altura de 9 m. Sabemos que o trabalho W realizado para levantar uma massa de água em uma altura h é dado por W = m g h , sendo m a massa de água e g o valor da aceleração da gravidade. Devemos então integrar a expressão d W = g h   d m , com d m sendo a massa de um disco de água de altura infinitesimal d z , para obtermos qual o trabalho que deve ser feito para erguer metade da água do tanque até o topo.

Passo 2

Vamos colocar o z o eixo vertical orientado pra cima com origem no fundo do tanque. Primeiro precisamos saber até que altura está a metade da água do tanque. O volume de um cone é dado por V = 1 3 π r 2 H , sendo H a altura do cone e r seu raio. Mas H = z , e podemos achar r em função de z por semelhança de triângulos, como mostra a figura.

4 10 = r z ⇒ r = 4 z 10 = 2 z 5

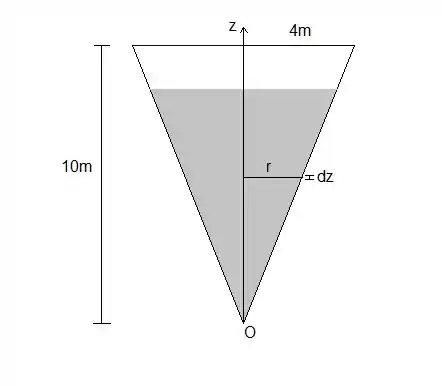
O volume fica então V z = 1 3 π 2 z 5 2 z = 4 75 π z 3 . O volume total da água é então V 9 = 4 75 π ⋅ 9 3 = 2916 75 π .

Passo 3

Agora que sabemos o volume total de água, podemos achar a partir de que altura a água será bombeada. Como V ( z ) = 4 75 π z 3 e V t o t a l = 2916 75 π :

V z = 1 2 V t o t a l ⇒ 4 75 π z 3 = 1 2 2916 75 π = 1458 75 π ⇒ 4 z 3 = 1458 ⇒ z 3 = 729 2 3 = 9 2 3

Então devemos integrar o trabalho infinitesimal d W de z = 9 2 3 até z = 9 .

Passo 4

Agora devemos achar a massa d m de um disco de água que está a uma altura z m do fundo do tanque. Ele terá uma altura infinitesimal d z e um raio r = 2 z 5 encontrado no passo 2. Seu volume será então d V = A d z = π 2 z 5 2 = 4 25 π z 2 d z . Sendo ρ = 1000   k g / m 3 a densidade da água, temos então d m = ρ d V = 1000 ⋅ 4 25 π z 2 d z = 160 π z 2 d z . Além disso, se o elemento está a uma altura z do fundo, será levantado uma altura de h = 10 - z . O trabalho infinitesimal realizado é então:

d W = g h   d m = g 10 - z ⋅   160 π z 2 d z = 160 π g   10 z 2 - z 3 d z

Passo 5

Agora podemos integrar para obter W :

W = ∫ 9 / 2 3 9 160 π g 10 z 2 - z 3 d z = 160 π g 10 z 3 3 - z 4 4 9 / 2 3 9 =

= 160 π g 10 ⋅ 9 3 3 - 9 4 4 - 10 ⋅ 9 2 3 3 3 - 9 2 3 4 4 =

= 160 π g ⋅ 7290 3 - 6561 4 - 7290 6 + 6561 8 2 3 ≈ 36108,8 π g

Se g = 9,81 m/s², temos W = 1112838   J

Resposta

1.112.838   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma tina cheia de água tem 10 m de comprimento e sua secção transversal tem a forma de um triângulo isósceles com 2 m de largura em cima e 2 m de altura. Qual o trabalho realizado para se bombear a ág
Um tanque cheio com água tem a forma de um paralelepípedo retangular com 5m de profundidade por 15 m de largura e por 25 m de comprimento. Ache o trabalho necessário para bombear a água no tanque a um
37) Uma força de 600 dinas estica uma mola de seu comprimento natural de 30 cm ate 35 cm ache o trabalho realizado ao se esticar a mola de seu comprimento natural ate 40 cm
36) Uma força de 2205,0 N é necessária pra comprimir uma mola de 25 cm até 22 cm. Ache o trabalho realizado para comprimir a mola até 20 cm.
36) Um cabo com 20 m e com uma densidade linear de 2 kg/m estar dependurado na vertical, ache o trabalho feito ao levantar todo o cabo.