Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.4 - Ex. 36

No exercício abaixo, realize uma divisão longa no integrando, escreva a fração própria como soma de frações parciais e então calcule a integral.

36 –

∫ 16 x 3 4 x 2 - 4 x + 1 d x

Passo 1

No primeiro passo realizaremos a divisão de polinômios:

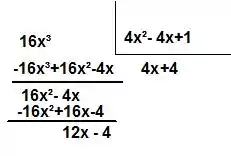
Assim temos:

∫ ( 4 x + 4 ) + 12 x - 4 4 x 2 - 4 x + 1 d x

Sendo: 4 x + 4 = 4 ( x + 1 )

Dado a propriedade matemática:

a - b 2 = a 2 - 2 a b + b 2

Assim para:

4 x 2 - 4 x + 1 = ( 2 x - 1 ) ²

Desta forma:

12 x - 4 2 x - 1 2 = A 2 x - 1 + B 2 x - 1 2

12 x - 4 = A 2 x - 1 + B

Resolvendo:

12 x - 4 = 2 A x - A + B

Igualando os coeficientes semelhantes de x, observe:

12 x = 2 A x , logo: A = 12 x 2 x ; A = 6

Igualando a constante:

- A + B =   - 4 , para A = 6

- 6 + B = - 4   ; B = 6 - 4   ; B = 2

Passo 2

Agora vamos substituir na Integral:

∫ 4 x + 1 d x + 6 ∫ 1 2 x - 1 d x + 2 ∫ 1 2 x - 1 2 d x

Resolvendo a primeira integral temos:

4 ∫ x + 1   d x = 4 x 2 2 + x = 4 x 2 2 + 4 x = 2 x 2 + 4 x

Resolvendo a segunda integral:

6 ∫ 1 2 x - 1 d x

t = 2 x - 1 ; d t = 2 ; d x = 1 d t = 1 2 ;

6 ⋅ 1 2 ∫ 1 t d t = 3 ∫ 1 t d t = 3 ln ⁡ t = 3 ln ⁡ 2 x - 1

Resolvendo a terceira integral:

2 ∫ 1 2 x - 1 2 d x

t = 2 x - 1 ; d t = 2 ; d x = 1 d t = 1 2 ;

Subsituindo:

2 ∫ 1 ( t 2 ) ⋅ 1 2 d t = 2 2 ∫ 1 t 2 d t =   ∫ 1 t 2 d t =   ∫ t - 2 d t = t - 2 + 1 - 2 + 1 = t - 1 1 = t - 1 = 1 t

Para t = 2 x - 1

Teremos:

1 2 x - 1

Passo 3

Juntando os resultados obtidos, teremos:

2 x 2 + 4 x + 3 ln ⁡ 2 x - 1 + 1 2 x - 1 + c

Resposta

2 x 2 + 4 x + 3 ln ⁡ 2 x - 1 + 2 x - 1 - 1 + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x
Utilize a tabela de integrais no fim do livro para calcular a integral ∫ d x 2 x 3 - 3 x 2
Escreva as formas de decomposição em frações parciais da função (como no exemplo 7). Não determine os valores númericos dos coeficientes. 2 .ax - 1 x 3 + x 2b x - 1 x 3 + x
Calcule a integral.int (x^2)/(x + 1) d x
Calcule a integral. ∫ y y + 2 d y