Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 62

No exercício, (a) ache a excentricidade, os focos e as diretrizes da cônica central dada. (b) faça um esboço mostrando a cônica, os focos e as diretrizes.

4 x 2 + y 2 = 64

Passo 1

Primeiro vamos manipula a equação para que ela fique em um formato que nós conhecemos e possamos separar as características da cônica a que se trata a equação dada na questão.

4 x 2 + y 2 = 64

4 x 2 64 + y 2 64 = 1

x 2 16 + y 2 64 = 1

x 2 4 2 + y 2 8 2 = 1

Da equação nesse formato já podemos retirar algumas informações: a cônica é uma elipse vertical centrada na origem, a = 8 , b = 4 . A última informação que precisamos é o coeficiente c, que pode ser calculado assim:

c 2 = a 2 - b 2

c 2 = 8 2 - 4 2

c 2 = 64 - 16

c 2 = 48

c = 48 = 4 3

Passo 2

Agora que já temos todas as informações necessárias sobre a cônica, precisamos apenas lembrar de como são definidos os pontos de uma elipse vertical:

e = c a = 4 3 8 = 3 2

F = 0 , c = ( 0 ,   4 5 )

F ' = 0 , - c = 0 , - 4 5

Agora é necessário lembrar da fórmula das retas diretrizes ( y 1 e y 2 ):

y 1 = a e = 8 3 / 2 = 16 3 = 16 3 3

y 2 = - a e = - 8 3 / 2 = - 16 3 = - 16 3 3

Passo 3

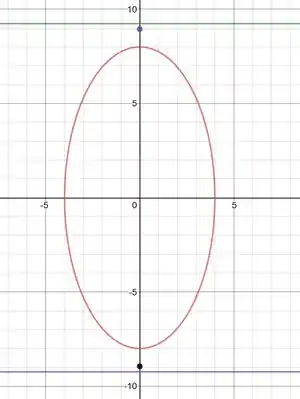
Agora que já sabemos todos os pontos importantes da elipse, basta marcá-los no plano cartesiano e ligar os pontos 😉

Resposta

e = 3 2

F = ( 0 ,   4 5 )

F ' = 0 , - 4 5

y 1 = 16 3 3

y 2 = - 16 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Coloque num gráfico o ponto com coordenadas polares - 3 ,- 2 3 π . Ache outro conjunto de coordenadas polares para esse ponto sendo (a) r0 e 0 ≤ θ2 π ; (b) r0 e - 2 π ≤ θ0 ; (c) r0e2 π ≤ θ4 π
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas21(c) ( - 4 ,2 3 π )
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas21(d) ( - 1 ,7 6 π )
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas21(a) ( 3 ,π )
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas21(b) ( 2 ,- 3 4 π )