Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 61

No exercício, (a) ache a excentricidade, os focos e as diretrizes da cônica central dada. (b) faça um esboço mostrando a cônica, os focos e as diretrizes.

25 x 2 - 9 y 2 = 225

Passo 1

Olhando para a equação da questão do jeito que ela está não é útil, nós aprendemos um formato de olhar pra equação de conicas de uma forma diferente, então vamos mexer nela de um jeito que, no final, nós vamos saber de qual cônica é essa equação.

25 x 2 - 9 y 2 = 225

25 x 2 225 - 9 y 2 225 = 1

x 2 9 - y 2 25 = 1

x 2 3 2 - y 2 5 2 = 1

Agora sim hein, depois de mexer um pouco, temos uma equação da qual é possível tirar algumas informações úteis: Ela se trata de uma hiperbole centrada na origem, a = 3 , b = 5 . Falta só aquele coeficiente c , lembra dele?

c 2 = a 2 + b 2

c 2 = 3 3 + 5 2

c 2 = 9 + 25 = 34

c = 34

Passo 2

Para terminar de responder a letra a, basta oranizar os dados que conseguimos descobrir a excentricidade, e os dois focos da hiperbole.

e = c a = 34 3

F = c , 0 = ( 34 , 0 )

F ' = - c , 0 = - 34 , 0

Agora é necessário lembrar da fórmula das retas diretrizes ( x 1 e x 2 ):

x 1 = a e = 3 34 3 = 1 34

x 2 = - a e = - 3 34 3 = - 1 34

Passo 3

Agora a questão ta na mão, vamos só fazer as marcações no sistema de coordenadas e ligar os pontos:

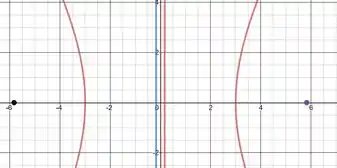
Resposta

e = 34 3

F = ( 34 , 0 )

F ' = - 34 , 0

Diretrizes:

x 1 = 1 34

x 2 = - 1 34

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 25 a 34, ache a equação polar do gráfico dada a sua equação cartesiana.26. x + y = 1
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas22(d) ( 2 ,- 7 6 π )
Nos exercícios 23 e 24, ache um conjunto de coordenadas polares dos pontos cujas coordenadas cartesianas retangulares são dadas. Tome r0 e 0 ≤ θ ≤ 2 π .24(d) ( - 2 ,- 2 3 )
Nos exercícios 23 e 24, ache um conjunto de coordenadas polares dos pontos cujas coordenadas cartesianas retangulares são dadas. Tome r0 e 0 ≤ θ ≤ 2 π .24(c) ( 0 ,- 2 )
Nos exercícios 23 e 24, ache um conjunto de coordenadas polares dos pontos cujas coordenadas cartesianas retangulares são dadas. Tome r0 e 0 ≤ θ ≤ 2 π .23(b) ( - 3 ,1 )