Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.3 - Ex. 2
No exercício a seguir, comprove que as hipóteses (i), (ii) e (iii) do Teorema de Rolle estão satisfeitas pela função dada no intervalo indicado. Ache então um valor “c” que satisfaça a conclusão do Teorema de Rolle.
Passo 1
Bom galera, temos que trabalhar neste exercício com o Teorema de Rolle. Tá, mas... qu rolê é esse? Hahahahah calma galera, vamos por partes que tudo se resolve!! O Teorema de Rolle, se baseia em três hipóteses e então em uma conclusão. Vamos para essas hipóteses:
Seja uma função f tal que:
- Ela seja contínua no intervalo fechado [a,b]
- Ela seja derivável no intervalo aberto (a,b)
Então exite um número c no intervalo aberto (a,b), tal que:
Não entendeu nada? Calma... vamos mastigar esse teorema JUNTOS!
Passo 2
A primeira hipótese fala da função ser continua no intervalo fechado [a,b]. Como é um polinômio super de boas, a gente sabe que: não só ele é continuo no intervalo fechado [a,b], como também é DERIVÁVEL no intervalo abeto (a,b)!!! QUE BOOOOOOM! Não está convencido(a) ainda? Vamos para o gráfico então:
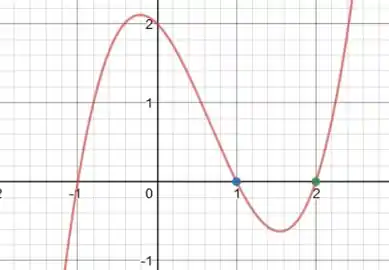
Tá vendo galerinha? A gente pode ver claramente que a função é contínua e derivável no nosso intervalinho dado! Portanto, hipótese (i) e (ii) comprovadíssimas!
Passo 3
Agora o pepino é provar a hipótese (iii)... SIMBORA! Aqui, temos que aplicar os valores dos intervalos, e verificar se a nossa função é igual a 0 nos pontos do nosso intervalo. E sim gente, eu sei que a gente pode ver ali em cima pelo gráfico que eles já são iguais a 0, mas vamos fazer as continhas, são fáceis .
Para o ponto em que , temos que:
E para o nosso segundo intervalo,:
Passo 4
Tamo quase lá galera! Então checamos que a nossa função é 0 para os dois pontos do intervalo. Portanto para matar a questão, basta achar a nossa conclusão. Para acharmos isso, temos que derivar nossa função e verificar se o nosso “c” realmente está dentro do intervalo! Vamo nessa!
Temos que o nosso f:
Derivando:
As raízes dessa equação correspondem a:
E sim, esses nosso dois pontos, estão no intervalo de ! Logo, TEOREMA MASTIGADO, DESTRUÍDO E PROVAAAADO!
Resposta
Ei, a resposta está no passo a passo :)