Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.2 - Ex. 8

Use o grafico dado no exercicio 7 para estimar os valores de c que satisfaçam à conclusao do teorema do valor medio pra

Passo 1

Faaaala meus lindões, aqui nessa questão devemos usar o gráfico de dado no exercício 7 que é o seguinte:

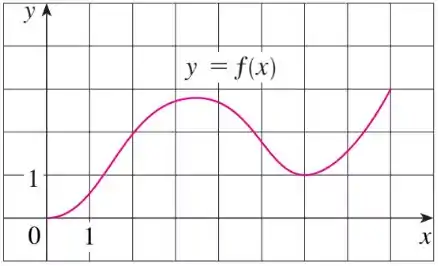
E então devemos traçar a reta secante dessa curva que intercepta os pontos extremos do intervalo que é .

Dessa forma, de acordo com o teorema do valor médio, existem valores de , onde a inclinação da reta tangente é igual a inclinação da reta secante que traçamos.

Essa é uma questão bem visual e sem conta. É mais sobre traçar retas mesmo.

Passo 2

Olhando para o nosso gráfico, podemos traçar a reta que vai de até para obter a nossa reta secante.

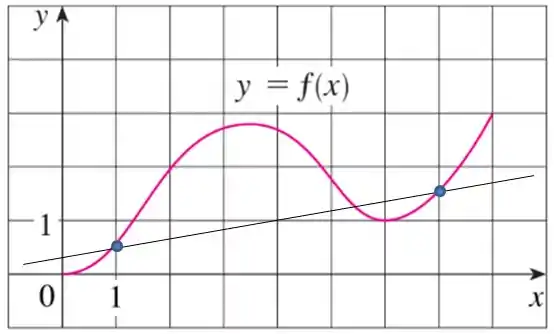
Passo 3

Agora vou traçar retas tangentes a minha função e ver em quais pontos essas retas tangentes tem inclinação igual a da reta secante.

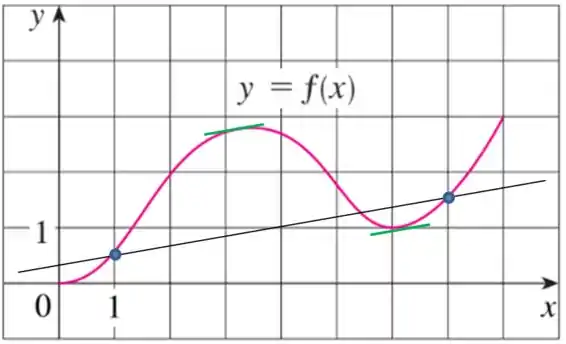
Agora, vamos ver quais são os valores de em que isso acontece.

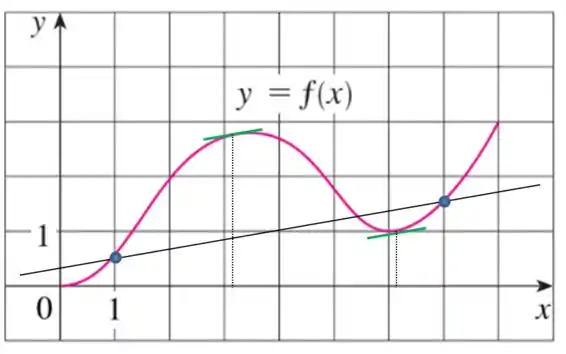
Vemos que assume os valores, aproximadamente:

Prontinho

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja g (x) = a r c t g x . Encontre f ( x ) , tal que f^' (x) = g ' ( x ) e f (1) = 2 .

Seja g (x) = x e^x - e^x . Encontre f ( x ) , tal que f^' (x) = g ' ( x ) e f (1) = 2 .

Use o Teorema do Valor Médio para mostrar que, se f for diferenciável em um intervalo aberto, e se f ' x ≥ M em cada x do intervalo, então f x - f y ≥ M | x - y | Com quaisquer x e y do intervalo.Use

Use o Teorema do Valor Médio para mostrar que y - xy - x 2 x Se 0xy .Use o resultado de (a) para mostrar que, se 0xy , então x y1 2 x + y . (a média aritmética é maior que a média geométrica)

Use o Teorema da Diferença Constante (4.8.3) para mostrar que, se f ' x = g ' ( x ) em cada x do intervalo ( - ∞ ,+ ∞ ) , e se f e g têm o mesmo valor em algum ponto x 0 , então f x = g ( x ) em cada