Encontre o número c que satisfaça à conclusão do Teorema do Valor Médio para o intervalo dado. Desenhe o gráfico da função, a reta secante passando pelas extremidades, e a reta tangente em (c, f (c)). A reta secante e a reta tangente são paralelas?

Para encontrar o número que satisfaz a conclusão do Teorema do Valor Médio para a função no intervalo primeiro calculamos a derivada da função para encontrar a taxa de variação instantânea.

A função pode ser reescrita como então sua derivada é:

Agora, aplicamos o Teorema do Valor Médio, que estabelece que existe pelo menos um número em tal que a taxa de variação instantânea nesse ponto é igual à taxa de variação média no intervalo.

A taxa de variação média no intervalo é dada pela diferença entre os valores de nos extremos do intervalo dividida pela diferença entre os extremos:

Agora, precisamos encontrar um em tal que Substituindo obtemos:

Para resolver isso, isolamos

Então, satisfaz a conclusão do Teorema do Valor Médio.

Agora, vamos desenhar o gráfico da função e as linhas secante e tangente.

O gráfico da função no intervalo é uma curva que começa em e sobe suavemente até

A reta secante será a reta que passa pelos pontos que é a reta que liga os extremos do intervalo.

A reta tangente em terá a mesma inclinação que a reta secante, pois o valor da derivada da função em é igual à taxa de variação média no intervalo.

Vamos desenhar esses elementos para visualização.

Primeiro, vamos calcular a inclinação da reta secante e a derivada da função em para encontrar a inclinação da reta tangente.

Inclinação da reta secante:

Derivada da função em

Portanto, a inclinação da reta secante e a derivada da função em são iguais, então a reta secante e a reta tangente são paralelas.

Agora, vamos desenhar o gráfico da função, a reta secante e a reta tangente.

Vamos começar desenhando o gráfico da função no intervalo

Vamos traçar a reta secante que passa pelos pontos e . A inclinação da reta secante é então podemos usar a equação ponto-inclinação da reta:

Substituindo e , obtemos:

Agora, vamos traçar a reta tangente em A inclinação da reta tangente também é , então a equação da reta tangente será a mesma que a reta secante.

No entanto, ela passa pelo ponto então não precisamos calcular a interceptação

O gráfico dessa função é representado da seguinte forma

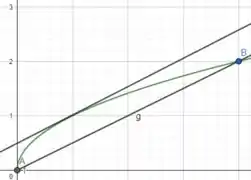
A reta secante é representada pela linha reta que liga . A reta tangente é uma linha reta que passa pelo ponto e tem a mesma inclinação que a reta secante.

Como previsto, a reta secante e a reta tangente são paralelas.