Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 2

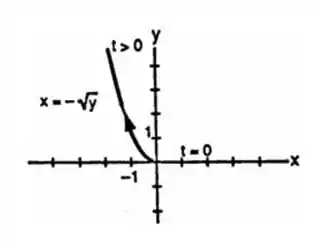
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano xy. Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o

Passo 1

Opa! E aí, tudo bem?! O enunciado nos deu as seguintes equações paramétricas:

Para o intervalo:

Essas equações representam a trajetória de uma partícula no plano .

O que a gente precisa fazer aqui é “desparametrizar” essas curvas, ou seja. Agora a gente tem e em função de e precisamos encontrar em função de , sacou?!

Depois disso a gente vai esboçar o gráfico da função que representa a trajetória da partícula!

Passo 2

Vamos começar isolando o parâmetro:

Agora só precisamos igualar ficando:

Passo 3

A trajetória da partícula é dada pela curva:

Lembrando que:

E o nosso intervalo é:

Sempre que teremos , então pra esboçar o nosso gráfico precisamos assumir valores apenas negativos de .

Dessa forma esboçando ficamos com:

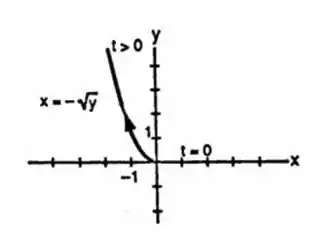
Prontinho!

Resposta

Exercícios de Livros Relacionados

Encontre equações paramétricas para a trajetória de uma partícula que se move ao longo do círculo x 2 + y - 1 2 = 4 Três vezes no sentido anti-horádio, a partir de ( 2,1 ) .

Encontre equações paramétricas para a trajetória de uma partícula que se move ao longo do círculo x 2 + y - 1 2 = 4 Uma vez no sentido horádio, a partir de ( 2,1 ) .

Trace a curva x = y - 3 y 3 + y 5

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.

Associe os gráficos das equações paramétricas x = f ( t ) y = g ( t ) Em a - ( d ) com as curvas paramétricas rotuladas de I - I V . Justifique.