Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 2
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da função no intervalo.
Passo 1
Seja . Vamos calcular
Como , então é crescente quando e decrescente quando .
Pelo mesmo motivo, quando logo é valor mínimo absoluto de . Além disso, quando , o que torna esse ponto crítico.
Passo 2
Calculando utilizando regra da derivada da divisão, teremos:
Logo, teremos que , ou seja, a função é sempre côncava para baixo. Logo é um ponto de máximo absoluto e valor máximo absoluto de .
Passo 3
Como já calculamos o comportamento da função, basta calcularmos os pontos de interseção da função com os eixos. Para isso, teremos:
Passo 4
Com todas essas informações extraídas, teremos:
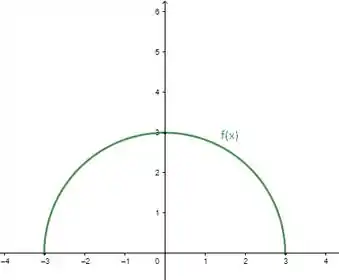
Resposta
Os valores absolutos da função são 0 (mínimo) e 3 (máximo). O mínimo acontece nos pontos e o máximo acontece no ponto . O esboço da função é:
