Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 28 b
Em cada parte, encontre todos os pontos críticos e uso e teste da derivada segunda (quando possível) para classifica-los em máximos ou mínimos relativos, ou em nenhum dos dois.
Passo 1
Sendo a função :
O primeiro passo para aplicar o teste da segunda derivada é encontrar a derivada da função, usando a derivação de um polinômio:
Analisando essa fórmula, sabemos que uma raiz está em :
O outro ponto crítico pode ser dado quando .
Passo 2
Agora, para continuar o teste da segunda derivada, derivamos a função mais uma vez:
Agora, devemos, analisar o valore da raiz em aplicado na segunda derivada:
Analisando o que foi explicado no exercício 23 do capítulo de revisão:
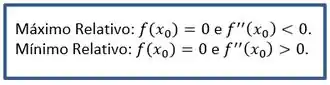
É portanto, um mínimo relativo.
Resposta
Mínimo Relativo:
Exercícios de Livros Relacionados
Uma caixa de base quadrada é mais alta do que larga. Para poder mandá-la pelo correio dos EUA, sua altura e o perímetro da base devem somar não mais que 108 polegadas. Qual é o volume máximo dessa cai
Um recipiente com a forma de um paralelepípedo com base quadrada deve ter um volume de 2 . 00 0c m 3 . O custo da base e da tampa é o dobro do custo dos lados. Encontre as dimensões do recipiente de m
Encontre um número no intervalo 1 2 , 3 2 tal que a soma do número com seu recíproco seja(a)a menor possível(b)a maior possível
Mostre que, dentre todos os retângulos com perímetro p , o quadrado é o que tem área máxima.
Um recipiente de base quadrada, lados verticais e aberto em cima deve ser feito de 90m 2 de material. Encontre as dimensões do recipiente com maior volume.