Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 25

A equação representa uma cônica degenerada. Identificá-la e esboçar o gráfico, quando possível.

x 2 - y 2 - 2 x - 2 y = 0

Passo 1

Vamos começar dando uma arrumada na equação e completar os quadrados:

x 2 - y 2 - 2 x - 2 y = 0

x 2 - 2 x - y 2 + 2 y = 0

Completando os quadrados:

x 2 - 2 x + 1 - 1 - y 2 + 2 y + 1 + 1 = 0

x - 1 2 - y + 1 2 = 0

Passando pro outro lado:

x - 1 2 = y + 1 2

Passo 2

Agora a gente tira os quadrados:

x - 1 = ± y + 1

Com o sinal de + :

x - 1 = y + 1

y = x - 2

E com o sinal de - :

x - 1 = - y - 1

y = - x

Assim, essa cônica na verdade é o conjunto de duas retas!

Passo 3

Esboçando:

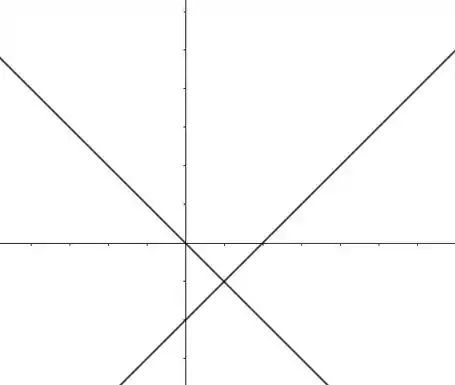
Resposta

Duas retas: y = - x e y = x - 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identificar as seguintes cônicas:x^2 - y = 1
Identificar as seguintes cônicas:x^2 - y = 0
Identificar as seguintes cônicas:x^2 - y^2 = 0
Identificar as seguintes cônicas:x^2 + y^2 = 0
Identificar as seguintes cônicas:x^2 + y^2 + 1 = 0