Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 16.2 - Ex. 16
Nos Exercícios 13-16, encontre as integrais de linha ao longo do caminho C dado.
Passo 1
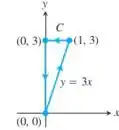
Fala galerinha tranquilidade, nessas questões nós teremos que calcular a integral proposta, no entanto esse é uma exercício que já faz a parametrização em relação a t, isso deixa a questões mais compreensível, caso contrário teriamos que parametrizar.
Passo 2
Nós precisamos substituir x e y na integral, pelo parâmetro t encontrado ficando, nesse caso como são três caminhos, nós teremos que fazer o mesmo procedimento para cada caminho.
Passo 3
Feita substituição podemos pegar a integral proposta e cálcular o seu valor:
Resposta
Exercícios de Livros Relacionados
É dado uma tabela com valores de uma função f com gradiente contínuo. Determine ∫ C ∇ f ⋅ r → , onde C tem equações paramétricas x = t 2 + 1 , y = t 3 + t, 0 ≤ t ≤ 1
Determine se F → é ou não um campo vetorial conservativo. Se for, determine uma função f tal que F → = ∇ f F → x , y = 2 x - 3 y i → + - 3 x + 4 y - 8 j →
O campo vetorial mostrado na figura é conservativo? Explique.
Este exercício ilustra a relação entre o vetor rotacional e rotações. Seja B um corpo rígido girando em torno do eixo z . A rotação pode ser descrita pelo vetor ω → = ω k → , onde ω é a velocidade ang
Determine (a) o rotacional e (b) o divergente do campo vetorial. F x , y , z = 1 x 2 + y 2 + z 2 xi + yj + zk