Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.3 - Ex. 25
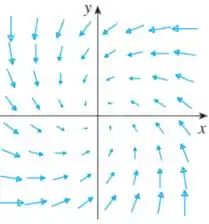
O campo vetorial mostrado na figura é conservativo? Explique.
Passo 1
Oi, galera! Tudo bem?
A questão nos deu essa figura e quer saber se ali há um campo conservativo ou não. Moleza, né?
Nós já estamos carecas de saber (ou deveríamos kkk) que quando um campo é conservativo, a integral de linha sobre qualquer curva fechada é zero:
Certo?
Passo 2
Vamos agora imaginar que a curva seja um círculo centrado na origem do desenho, orientada no sentido anti-horário, assim ó:
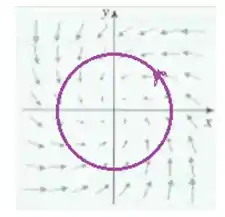
Podemos ver que todos os vetores que começam em são no sentido do movimento, então a integral sobre essa curva será positiva. Com isso:
Portanto, esse campo não é conservativo!
Resposta
Exercícios de Livros Relacionados
Determine (a) o rotacional e (b) o divergente do campo vetorial. F x , y , z = e x y sen z j + y tg - 1 x z k
Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = x y z 2i + x 2 y z 2j + x 2 y 2 zk
O campo vetorial F é mostrado no plano x y e é o mesmo em todos os planos horizontais (em outras palavras ,F é independente de z e sua componente z é 0 ).O d i vF será positivo, negativo ou nulo? Expl
Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F → = ∇ f F → x , y , z = y 2 z 3i ^ + 2 x y z 3j ^ + 3 x y 2 z 2k ^
Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = 2 x yi + x 2 + 2 y z j + y 2k