Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.8 - Ex. 4
Nos Exercícios 1-4:
a. Determine .
b. Esboce em um único gráfico e
c. Calcule em e em para mostrar que nesses pontos .
4.
Passo 1
a.
Para determinarmos sua inversa devemos, simplesmente, isolar o :
A raiz quadrada é positiva, pois o enunciado nos diz que .
Então,
Passo 2
b.
Os dois gráficos são simples de desenhar por serem bastante conhecidos. O primeiro uma função do segundo grau só definida para positivo e o segundo uma função raiz quadrada.
Podemos plotar alguns pontos, para termos um gráfico mais fiel. E vamos obter:
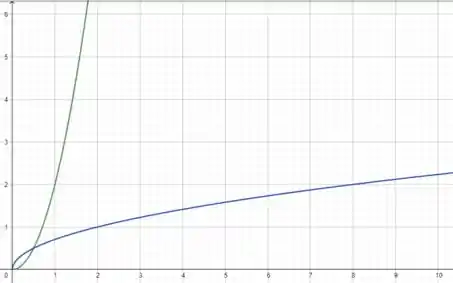
Passo 3
c.
A derivada da função é simples de ser calculada, pois é um polinômio bem simples:
Para acharmos a derivada no ponto é só substituir na função da derivada:
Passo 4
c.
A derivada da função inversa também é fácil por também ser um polinômio simples:
Para :
Substituindo na derivada da inversa:
Passo 5
c.
Portanto no ponto , a relação
é valida, pois
Resposta
a. b.
c.