Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 14

Nos Exercícios de 1 a 16, encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico e mostre um segmento da reta tangente ao gráfico nos pontos de inflexão.

1 4 )   f x = 3 . c o s   2 x ;     x ∈ [ - π , π ]  

Passo 1

Para começar precisamos determinar os pontos de inflexão do gráfico, ou seja, o ponto onde a função muda a direção da concavidade. Para descobrir estes pontos o primeiro passo é descobrir a derivada segunda da nossa função:

f x = 3 . c o s   2 x

f ' x = 0 . c o s   2 x - 2.3 . s en ⁡ 2 x = - 6 sen ⁡ 2 x

f ' ' x =   0 . sen ⁡ 2 x - 6 . 2 . c o s   2 x = - 1 2 . c o s   2 x

Uma vez descoberta a derivada segunda, os pontos de inflexão são caracterizados por f ' ' x = 0 .

Passo 2

Igualando f ' ' x = 0 :

- 12 . c o s   2 x = 0

Para que a função cosseno seja igual a 0:

2 x = π 2 → x = π 4

2 x = - π 2 → x = - π 4

Como a função é periódica:

x = 3 π 4       o u       x = - 3 π 4

Para determinar se existe ou não um ponto de inflexão nestes pontos, precisamos verificar se f ' ' x muda de sinal.

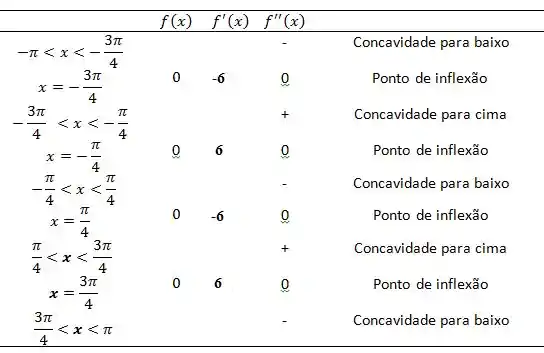
Sendo assim,   x = π 4 ,   x = - π 4 ,     x = 3 π 4   e     x = - 3 π 4 são pontos de inflexão.

Desenhando o gráfico da função e traçando as retas tangentes aos pontos de inflexão:

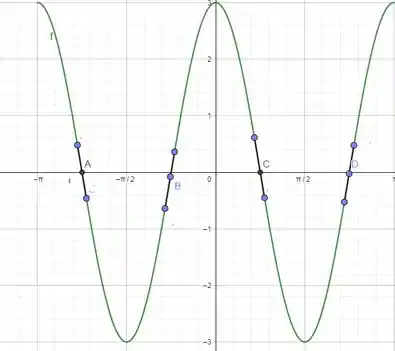
Resposta

Pontos de inflexão: x = π 4 ,   x = - π 4 ,     x = 3 π 4   e     x = - 3 π 4 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se f x = a x 3 + b x 2 , determine a e b de tal forma que o gráfico de f tenha um ponto de inflexão em ( 2 ,16 ) .
Ache o ponto (ou pontos) de inflexão do gráfico da função definida por f x = 2 - x 2 ,s ex0 x 2 + 2 ,s ex ≥ 0 e determine onde o gráfico é côncavo para cima e côncavo para baixo.
Ache o ponto (os pontos) de inflexão do gráfico da função definida por f x = x 1 5 e determine onde o gráfico é côncavo para cima e onde é côncavo para baixo.
Se f x = a x 3 + b x 2 + c x , determine a , b e c de tal forma que o gráfico de f tenha um ponto de inflexão em ( 1 ,- 1 ) e que a inclinação da tangente inflexional seja - 3 .
Se f x = x | x | , mostre que o gráfico de f tem um ponto de inflexão na origem.