Nos exercícios de 21 a 26, ache uma nova equação para o gráfico da equação dada após uma translação de eixos para a nova origem, conforme está indicado. Trace os eixos originais e os novos e faça um esboço do gráfico.
Passo 1
Um ponto representado por em relação ao sistema de eixos anterior, tem representação em relação ao novo sistema de eixos que queremos mostrar. Com isso, podemos dizer que:
Agora vamos substituir isso na nossa equação.
Passo 2
Assim podemos ver que a nossa figura está no centro dos nossos novos eixos
Passo 3
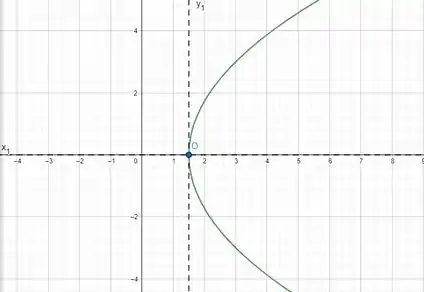
Na figura podemos ver onde se encontrava nosso gráfico nos eixos antigos. Agora com os novos eixos e representados pela linha tracejada, a parábola se encontra centrado na origem dos novos eixos.