Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 35

Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada

A parte da esfera x 2 + y 2 + z 2 - 4 z = 0 que está acima do plano z = 2

Passo 1

x 2 + y 2 + z 2 - 4 z = 0

Vamos começar reorganizando a equação e complementando os quadrados

x 2 + y 2 + z 2 - 4 z + 4 = 0 + 4

x 2 + y 2 + z - 2 2 = 2 2

É a esquação de uma esfera, com raio a = 2 e centrado no ponto r c = ( 0,0 , 2 ) .

Passo 2

A equação paramétrica da esfera é:

r → ( u , v ) e s f e r a   n a o r i g e m = a cos ⁡ v cos ⁡ u i → + a cos ⁡ v sen ⁡ u j → + a sen ⁡ v k →

Com os limites máximos definidos como

0 ≤ u ≤ 2 π

- π 2 ≤ v ≤ π 2

Para uma esfera centralizada em um ponto qualquer a equação é:

r → ( u , v ) = r → ( u , v ) e s f e r a   n a o r i g e m + r → c

Substituíndo os valores do raio e a centralização da esfera

r → u , v = 2 cos ⁡ v cos ⁡ u i → + 2 cos ⁡ v sen ⁡ u j → + ( 2 + 2 sen ⁡ v ) k →

As componentes são:

x = 2 cos ⁡ v cos ⁡ u

y = 2 cos ⁡ v sen ⁡ u

z = 2 + 2 sen ⁡ v

Passo 3

Observe que a esfera está centrada exatamente no plano. Então, a região acima do plano é o hemisfério superior da esfera:

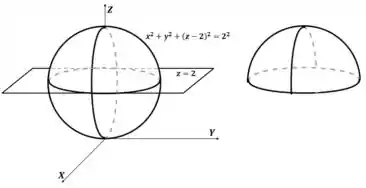
Então, podemos redefinir os limites dos ângulos u e v para que se limitem ao hemisfério superior.

O ângulo u determina o giro em torno do eixo Z, então este continua tal qual a equação geral da esfera.

0 ≤ u ≤ 2 π

Já o ângulo v deve ser limitado a sua parte positiva:

0 ≤ v ≤ π 2

Resposta

x = 2 cos ⁡ v cos ⁡ u

y = 2 cos ⁡ v sen ⁡ u

z = 2 + 2 sen ⁡ v

0 ≤ u ≤ 2 π

0 ≤ v ≤ π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas da grade que têm u constante e quais têm v constante. x = se
Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = s
Encontre as representações paramétricas das superfícies:A parte do cilindro x 2 + z 2 = 9 que está acima do plano x y e entre os planos y = - 4 e y = 4 .
Encontre as representações paramétricas das superfícies:A parte da esfera x 2 + y 2 + z 2 = 36 que está entre os planos z = 0 e z = 3 3 .
Encontre a área da superfície com precisão de quatro casas decimais, expressando-a em termos de uma integral unidimensional e usando sua calculadora para estimar a integral.A parte da superfície z = l