Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 29
Nos Exercícios de 29 a 31:
- Ache os pontos de inflexão do gráfico da função trigonométrica dada;
- Ache a inclinação das retas tangentes nos pontos de inflexão;
- Faça um esboço do gráfico da função num intervalo de de comprimento e contendo o ponto de inflexão com menor abscissa positiva, e mostre um segmento da reta tangente nesse ponto de inflexão.
Passo 1
Para a letra a precisamos determinar os pontos de inflexão do gráfico, ou seja, o ponto onde a função muda a direção da concavidade, devemos obter a derivada segunda da nossa função:
Uma vez descoberta a derivada segunda, os pontos de inflexão são caracterizados por . Então:
Para que essa igualdade seja satisfeita:
Analisando a mudança da concavidade:
Então, para k inteiro os valores de são pontos de inflexão.
Passo 2
Na letra b, precisamos lembrar que a inclinação das retas tangentes é dada pela derivada primeira da função. Sendo assim:
Para os pontos de inflexão:
A inclinação da reta tangente no ponto
E no ponto
Generalizando para todo k:
Passo 3
Na letra c, desenhamos a função co-seno no intervalo de 0 até e traçamos a reta tangente no ponto de inflexão com menor abscissa positiva ().
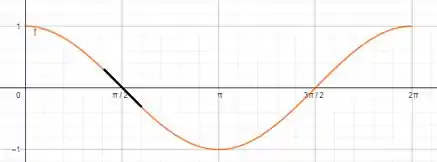
Resposta
- Pontos de inflexão:
- Inclinação da reta tangente