Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 33
Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.
33. Vértice em ; foco em .
Passo 1
Pelos pontos dados no enunciado para o vértice e o foco é possível ver que eles estão na mesma reta .
Com essa informação podemos tirar que a parábola está deitada, então sua equação é algo do tipo:
Olhando as coordenadas do vértice e do foco, vemos que o foco está a esquerda do vértice, logo a parábola tem concavidade para esquerda, assim a equação acima fica:
Agora precisamos achar os valores de h, p e k para a situação que temos.
Passo 2
Achar h e k é fácil, eles representam as coordenadas do vértice.
O h representa a coordenada y do vértice e k a coordenada x, logo:
Passo 3
Agora vamos achar o p, para isso precisamos lembrar que a distância entre o vértice e o foco é igual a p.
Como o vértice e o foco estão na mesma reta , a distância entre eles vai ser dada pela diferença entre as coordenadas x do vértice e do foco. Assim:
Passo 4
Agora colocando tudo que encontramos na equação ela toma a seguinte forma:
Passo 5
O gráfico que representa a equação da parábola é da seguinte maneira:
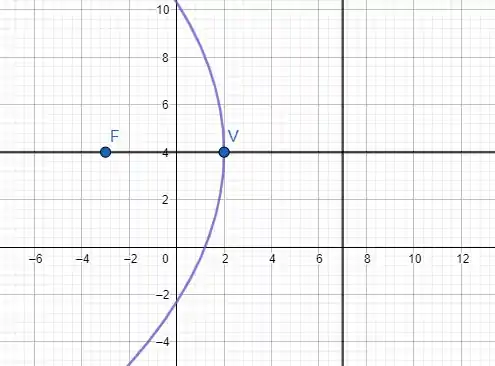
Resposta
Ei, a resposta está no passo a passo :)