Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 34
Nos Exercícios de 33 a 40, ache uma equação da parábola com as propriedades dadas. Faça um esboço do gráfico.
34. Vértice em ; diretriz .
Passo 1
Pela equação da reta diretriz dada é possível ver que ela é paralela ao eixo x.
Com essa informação podemos tirar que a parábola está em pé, então sua equação é algo do tipo:
Olhando a localização do vértice e a posição da reta diretriz, é possível ver que o vértice está abaixo da reta diretriz, assim a parábola não pode ter concavidade para cima, se não ela iria passar pela reta diretriz, coisa que não faz sentido, logo ela tem concavidade voltada para baixo. Assim nossa equação acima fica:
Agora precisamos achar os valores de h, p e k para a situação que temos.
Passo 2
Achar h e k é fácil, eles representam as coordenadas do vértice.
O h representa a coordenada x do vértice e k a coordenada y, logo:
Passo 3
Agora vamos achar o p, para isso precisamos lembrar que a distância entre o vértice e a reta diretriz é igual a p.
Como sabemos que a reta diretriz é para todo x, para achar o p basta fazer a diferença entre a coordenada y do vértice e a reta diretriz, assim:
Passo 4
Agora colocando tudo que encontramos na equação ela toma a seguinte forma:
Passo 5
O gráfico que representa a equação da parábola é da seguinte maneira:
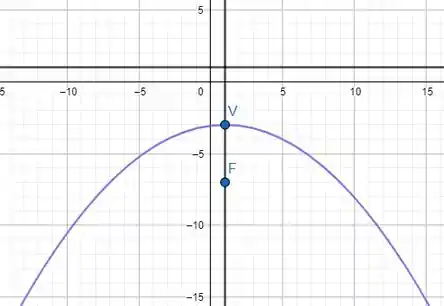
Resposta
Ei, a resposta está no passo a passo :)