Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 41

Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.

41. f x ,   y = 2 + x + 3 y ; x ≥ 0 , y ≥ 0 e x + y ≤ 1 .

Passo 1

Então galera, se esboçarmos o gráfico que representa o domínio que queremos analisar, teremos:

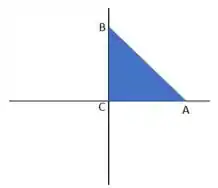
Esse problema facilita bastante a nossa vida, uma vez que não há pontos críticos no interior da figura, uma vez que as derivadas parciais são constantes. Além disso, também não há pontos críticos na fronteira, se liga:

z = 2 + x + 3 y

Sabendo que x + y = 1 , então:

z = 2 + 1 - y + 3 y

z = 3 + 2 y

Derivando:

z ' = 2

Dessa forma, só precisamos analisar os vértices do triângulo de fato.

Passo 2

Substituindo os pontos dos vértices na nossa função, teremos:

f 0 ,   0 = 2   ( m í n i m o )

f 1 ,   0 = 2 + 1 = 3

f 0 ,   1 = 2 + 3 = 5   ( m á x i m o )

Dessa forma, podemos concluir que o ponto ( 0 ,   0 ) é ponto de mínimo e tem valor de 2 e o ponto ( 0 ,   1 ) é ponto de máximo e tem valor de 5 .

E está aí nossa análise, galera! 😉

Resposta

Ponto de mínimo: ( 0 ,   0 ) , valor: 2 ;

Ponto de máximo: ( 0 ,   1 ) , valor: 5 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores máximo e mínimo absolutos de f no conjunto D. f x , y = x 2 + x y + y 2 - 6 y ,D = x , y - 3 ≤ x ≤ 3 ,0 ≤ y ≤ 5 }
Determine os valores máximo e mínimo absolutos de f no conjunto D. f x , y = x 2 + 2 y 2 - 2 x - 4 y + 1D = x , y 0 ≤ x ≤ 2 ,0 ≤ y ≤ 3 }
Determine os valores máximo e mínimo absolutos de f no conjunto D. f x , y = x y 2D = x , y x ≥ 0 ,y ≥ 0 ,x 2 + y 2 ≤ 3 }
Se o comprimento da diagonal de uma caixa retangular deve ser L , qual é o maior volume possível.
Encontre os valores máximos e mínimos absolutos de f no conjunto D . f x , y = x 3 - 3 x - y 3 + 12 y , D é um quadrilátero com vértices: ( - 2,3 ) , ( 2,3 ) , ( 2,2 ) e ( - 2 , - 2 )