Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 37

Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.

37. ; no triângulo de vértices e .

Passo 1

Então pessoal, esboçando o triângulo em questão, teremos:

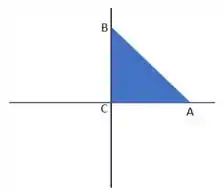
Inicialmente vamos analisar se há pontos críticos no interior da região em questão, tudo bem? Para isso, teremos que derivar parcialmente a função que nos foi dada para depois iguala-la a zero, se liga:

Igualando a zero, teremos:

Sendo assim, temos que o ponto é um ponto crítico no interior do triângulo.

Passo 2

Para classificarmos se o ponto crítico que encontramos é ponto de máximo, mínimo ou se é ponto de sela, devemos encontrar o determinante Hessiano, dado da seguinte forma:

Então temos que encontrar essas derivadas parciais aí! Sendo assim:

Substituindo, teremos:

Dessa forma, pelas proposições estudadas, temos que se o determinante resulta em um valor positivo, assim como a derivada parcial de segunda ordem, então o ponto em questão é um ponto de mínimo!

Passo 3

Ufa! A primeira parte da análise foi concluída, que é a análise do interior. Agora teremos que analisar a fronteira, ou melhor, cada segmento de reta do triângulo.

Para o segmento temos que , então , . Sendo assim, teremos:

Derivando e igualando a zero:

Sendo assim, para esse valor de :

Se substituirmos o ponto na função que nos foi dada, notaremos que se trata de um mínimo.

Passo 4

Para o segmento temos que , então . Sendo assim, teremos:

Derivando e igualando a zero:

Se substituirmos o ponto na função que nos foi dada, notaremos que se trata de um mínimo.

Para o segmento temos que , então . Sendo assim, teremos:

Derivando e igualando a zero:

Se substituirmos o ponto na função que nos foi dada, notaremos que se trata de um mínimo. Em resumo, o ponto é um ponto de mínimo e apresenta valor de e o ponto é um ponto de máximo e apresenta valor de .