Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 36
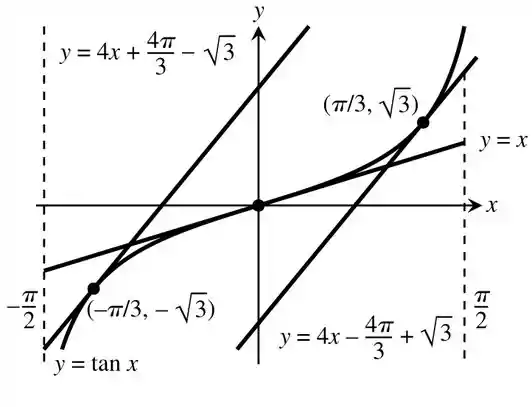
Nos Exercícios 35-38, represente graficamente as curvas nos intervalos dados e suas respectivas tangentes para os valores dados de . Identifique cada curva e tangente com a sua equação respectiva.
36.
Passo 1
Sabemos que o coeficiente angular da reta tangente, a certo ponto de uma função, é numericamente igual a derivada da função nesse ponto.
Então para sabermos a inclinação das retas tangentes ao pontos vamos calcular a derivada nesses pontos.
A equação da reta é da forma:
Onde A é sua inclinação ou coeficiente angular, que como já calculamos vale 4 para as duas retas.
Para descobrirmos o valor de só precisamos colocar uma valor para que pertença a reta. Como essas retas são tangentes a função nos pontos vamos usa-los:
No ponto:
Portanto temos o ponto e , calculando :
Logo a equação dessa reta é:
No ponto:
Portanto temos o ponto e , calculando :
Logo a equação dessa reta é:
O gráfico vai ficar dessa forma:
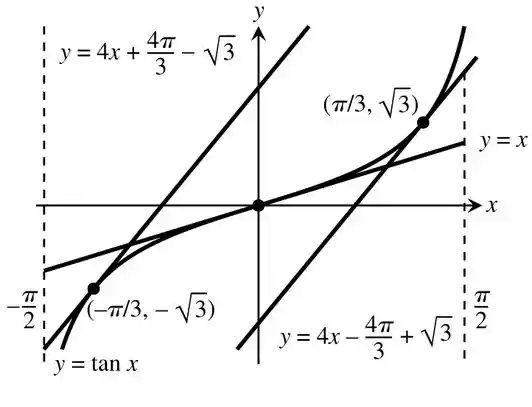
Resposta
