Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.4 - Ex. 25
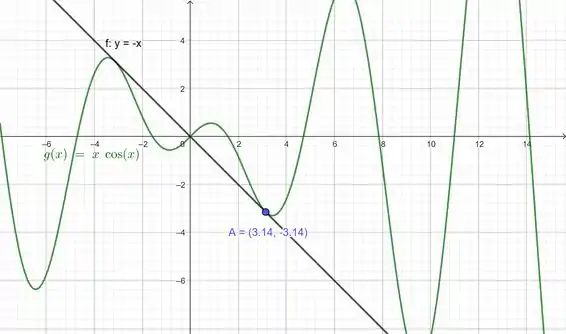
25.(a) Encontre uma equação da reta tangente à curva no ponto
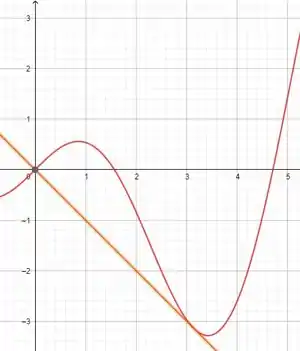
(b) Ilustre a parte (a) fazendo o gráfico da curva e a reta tangente na mesma tela.
Passo 1
Olá, meu amigo. Vamos resolver essa atividade.
Aqui a gente tem a função:
E queremos calcular a reta tangente a esta curva no ponto .
Quando a gente fala de equação da reta tangente, precisamos falar sobre derivadas. O coeficiente angular da reta é dado por:
Assim como a equação da reta dado um ponto e coeficiente angular!
Onde o ponto vai ser o ponto .
Passo 2
Vamos fazer a derivada, vamos usar o produto de derivada então, vamos relembrá-lo. Nunca é demais relembrar fórmulas!!
Fazendo aquela anotação esperta de e :
Substituindo na expressão que está escrita no comecinho!
Passo 3
Vamos com calma! Primeiro vamos achar o coeficiente angular, que é bem simples, apenas temos que substituir por na expressão da derivada!
Usaremos agora a equação da reta, dessa forma e lembrando que o ponto é esse aqui :
(b) Gerando o gráfico com ajuda do GeoGebra, podemos ver que estamos certos nos nossos cálculos.
Resposta
(a)
(b) 
