Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 15
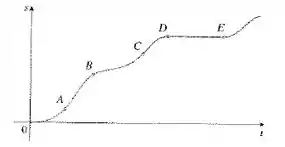
O gráfico ilustra a função posição de um carro. Use a forma do gráfico para explicar suas respostas para a seguinte questão.
- Qual a velocidade inicial do carro?
- O carro está mais rápido em B ou C?
- O carro está aumentando ou diminuindo a rapidez em A, B ou C?
- O que aconteceu entre D e E?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente usar o gráfico dado para explicar a velocidade inicial do carro, os locais onde o carro está mais rápido, os locais onde ele está aumentando ou diminuindo a rapidez e o que acontece em determinados pontos.
O gráfico dado foi esse aqui:
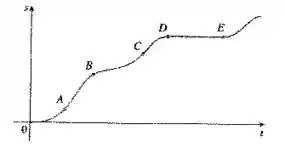
Observe que ele representa a curva de variação do espaço em função do tempo . E todas as informações que o enunciado pede pra gente encontrar dizem respeito a velocidade do carro. E nós sabemos que a velocidade média é justamente a taxa de variação da posição de uma partícula em função do tempo e que ela pode ser representada pela inclinação da reta tangente nesse ponto.
Então, o que nós vamos fazer é desenhar a reta tangente em cada ponto que deve ser analisado e determinar o que cada item do enunciado pede, com base na inclinação dessa reta.
Vamos lá!
Passo 2
Para o item (a) precisamos determinar a velocidade inicial do carro, isto é, a velocidade no tempo , que é a origem do nosso plano cartesiano.
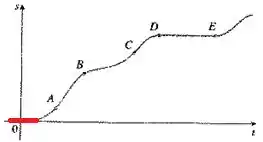
Desenhando uma reta tangente nesse ponto, nós observamos que a reta não tem inclina��ão, porque ela é horizontal, e como a inclinação é zero, podemos dizer que a velocidade inicial do carro é .
Chamando essa velocidade inicial de , temos:
Passo 3
Para a letra (b) queremos saber se ele é mais rápido em ou em . Como fazemos isso?
Nós aplicamos uma reta tangente em e em , certo? Vamos ver:
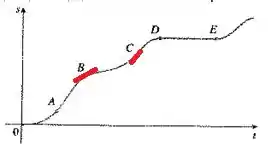
Observe que no ponto , temos uma reta mais inclinada do que em , parece que ela tá subindo uma ladeira mais íngreme, sabe?
E como a inclinação representa a taxa de variação da posição em função do tempo, que é a velocidade, podemos dizer que em o carro está mais rápido do que em .
Se a gente chamar a velocidade em de e a velocidade em de , temos que:
Passo 4
A letra (c) quer saber se o carro está aumentando ou diminuindo a rapidez em , ou . Então, vamos analisar a reta tangente em cada um desses pontos:
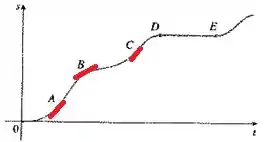
Pra dizer se o carro está aumentando ou diminuindo a rapidez, que é a velocidade, temos que analisar a inclinação dessas retas.
Vemos que perto de , as linhas tangentes estão se tornando mais íngremes à medida que aumentam. Isso significa que a velocidade estava aumentando, então o carro estava acelerando nesse ponto.
Perto de , as linhas tangentes estão se tornando menos íngremes, é como se ele estivesse começando a descer a ladeira. Então, o carro estava desacelerando, logo a velocidade é baixa.
Já em , vemos que a reta tangente é a mais acentuada, mais inclinada. Portanto, em, o carro havia acabado de acelerar e estava prestes a começar a desacelerar.
Passo 5
Por fim, vamos analisar o que aconteceu entre e .
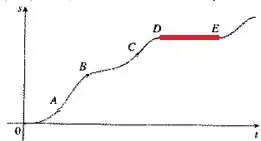
Percebemos que existe uma reta horizontal entre esses dois pontos. Isso significa que a inclinação da reta tangente é . Dessa forma, podemos dizer que o carro não se moveu durante esse tempo.
Valeu, galera! Até a próxima! 😉
Resposta
- a velocidade inicial do carro é ;
- em , a inclinação da reta tangente é maior, logo, ele é mais rápido;
- em , o carro estava acelerando; em , estava desacelerando e em , havia acelerado e estava prestes a desacelerar.
- O carro não se moveu nesse tempo.