Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.5 - Ex. 48

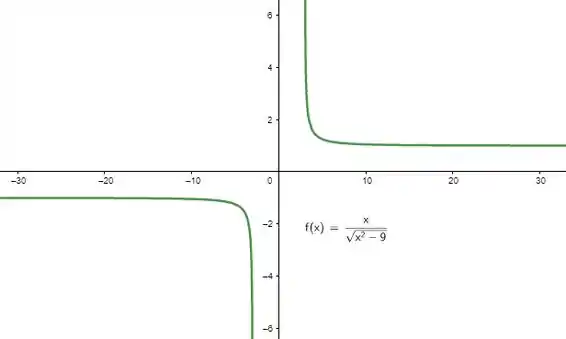
Nos exercícios de 37 a 48, encontre as assíntotas horizontal e vertical e trace um esboço do gráfico da função

48 )   h x = x x 2 - 9

Passo 1

Pra achar as assíntotas horizontais precisamos fazer os limites pros infinito, beleza?

lim x → ± ∞ ⁡ x x 2 - 9 = lim x → ± ∞ ⁡ x x 2 1 - 9 x 2 = lim x → ± ∞ ⁡ x x ∙ 1 - 9 x 2

Pra x → + ∞

lim x → ± ∞ ⁡ x x ∙ 1 - 9 x 2 = lim x → + ∞ ⁡ x x ∙ 1 - 9 x 2 = lim x → + ∞ ⁡ 1 1 - 9 x 2 = 1 1 - 0 = 1

Pra x → - ∞

lim x → - ∞ ⁡ x x ∙ 1 - 9 x 2 = lim x → + ∞ ⁡ - x x ∙ 1 - 9 x 2 = lim x → + ∞ ⁡ - 1 1 - 9 x 2 = - 1 1 - 0 = - 1

Limites deram números? Então beleza, temos assíntotas horizontais!

Passo 2

Pras verticais, fazemos os limites pros pontos que “dão problema”. No caso eles vão ser x = ± 3 porque h ± 3 não está definido, já que zeram o denominador. Vamos ter:

lim x → 3 ⁡ x x 2 - 9 = 3 0 + = + ∞

lim x → - 3 ⁡ x x 2 - 9 = - 3 0 + = - ∞

Se os limites explodiram então temos duas assíntotas verticais

Passo 3

Juntando os resultados dos limites, esboçamos:

lim x → + ∞ ⁡ x x 2 - 9 = 1

lim x → - ∞ ⁡ x x 2 - 9 = - 1

lim x → 3 ⁡ x x 2 - 9 = + ∞

lim x → - 3 ⁡ x x 2 - 9 = - ∞

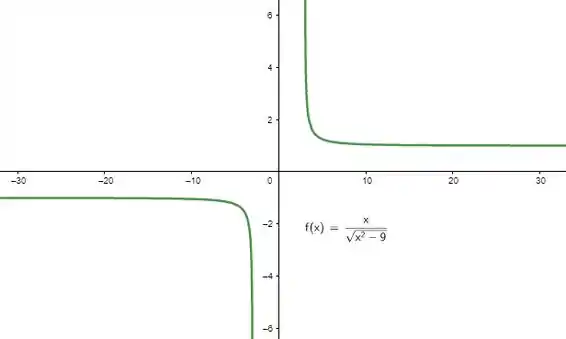
Resposta

lim x → + ∞ ⁡ x x 2 - 9 = 1

lim x → - ∞ ⁡ x x 2 - 9 = - 1

lim x → 3 ⁡ x x 2 - 9 = + ∞

lim x → - 3 ⁡ x x 2 - 9 = - ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o limite lim x → ∞ ⁡2 x+3 5 x+7
Determine o limite lim x → - ∞ ⁡2 x 2 +3 5 x 2 +7
Determine o limite lim τ → ∞ ⁡ ln ⁡ 1+1 τ
Determine o limite lim x → ∞ ⁡ t g - 1 ⁡ ( x )
Determine o limite lim x → ∞⁡ e 1 x∙c o s 1 x