Nos Exercícios de 1 a 40, faça o seguinte: (a) ache os extremos relativos de f pelo teste da primeira derivada; (b) determine os valores de x nos quais os extremos relativos ocorrem; (c) determine os intervalos nos quais f é crescente; (d) determine os intervalos nos quais f é crescente; (e) faça um esboço do gráfico.
40.
Passo 1
Basicamente quase tudo nesse exercício depende de analisarmos a derivada da função e os intervalos onde ela é positiva, negativa e zero.
E usaremos o Teorema 4.4.4 do Capítulo 4, Seção 4 do livro.
Passo 2
Vamos derivar a função fornecida pelo enunciado.
Passo 3
Agora vamos analisar para qual valores de x a primeira derivada zera.
Para que a expressão acima seja igual a zero, temos que:
Passo 4
Então achamos o valor de x que é ponto crítico de , que é . Agora vamos ver o valor de para tal ponto, jogando o x que encontramos na nossa função.
Passo 5
Agora vamos avaliar para quais intervalos é crescente e decrescente, para isso precisamos ver para quais valores de x é positiva e para quais valores ela é negativa.
Vemos que para:
Olhando essas avaliações você pode ver que é extremo relativo de , pois como apresenta uma descontinuidade ele é número crítico de .
Então segundo o teorema 4.4.4, como a função é crescente antes de e decrescente depois do mesmo, logo é ponto máximo, como a função é decrescente antes de e crescente depois do mesmo, logo é ponto mínimo.
Abaixo temos os resultados resumidos em uma tabela.

Passo 6
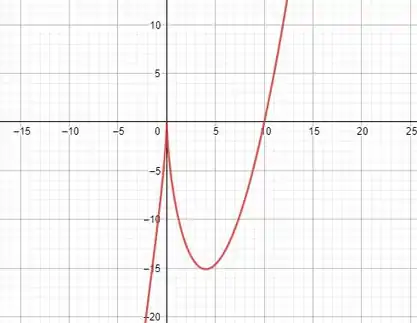
Abaixo podemos ver o gráfico da função.
Resposta
- , são extremos relativos.
- Em , em ocorre extremo relativo.
- é crescente em ,
- é decrescente em