Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.1 - Ex. 6

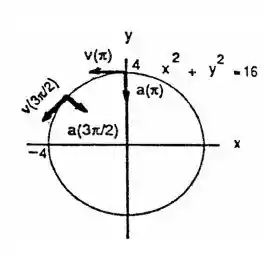
Os Exercícios 5-8 fornecem os vetores posição de partículas que se movem ao longo de diversas curvas no plano xy. Em cada caso, encontre os vetores velocidade e aceleração da partícula nos instantes indicados e esboce-os como vetores na curva.

Passo 1

Fala galerinha tranquilidade, seguinte para esse primeiro passo nós iremos encontrar a velocidade vetorial da partícula, isso pode ser feito derivando a posição em relação ao tempo:

Como são vetores derivamos cada componente:

Passo 2

Nesse passo vamos encontrar a aceleração da partícula, que pode ser feito derivando duas vezes a posição ou derivando a velocidade, nós iremos derivar a velocidade:

Como são vetores derivamos cada uma das componentes:

Passo 3

Sabendo velocidade e aceleração dos dois primeiros passos, agora vamos calcular nos instantes de tempo que o problema pediu:

Resposta

Agora o esboço da curva é uma círculo de raio 4:

Exercícios de Livros Relacionados

Uma partícula se desloca no espaço. Em cada instante t o seu vetor posição é dado por r → t = t i → + 1 t - 2 j → + k → Determinar a posição da partícula no instante t = 0 e t = 1 ;Esboçar a trajetóri

Mostrar que a função vetorial f → t = f 1 t i → + f 2 t j → + f 3 ( t ) k → é contínua em um intervalo I se, e somente se, as funções reais f 1 t ,f 2 t ef 3 ( t ) são contínuas em I .

Indicar os intervalos de continuidade das seguintes funções vetoriais:f) r → t = e t , t 2 - 1 t - 1 , ln ⁡ t + 1

Indicar os intervalos de continuidade das seguintes funções vetoriais:d) v → t = ln ⁡ t + 1 , 1 t ,t

Sejam f → e g → funções vetoriais contínuas em um intervalo I . Mostrar que:a) f → + g → é contínua em I .