Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 5
Uma partícula se desloca no espaço. Em cada instante o seu vetor posição é dado por
- Determinar a posição da partícula no instante e ;
- Esboçar a trajetória da partícula;
- Quando se aproxima de , o que ocorre com a posição da partícula?
Passo 1
Gente, para encontrarmos a posição da partícula nos instantes e , como pedido na letra (a), basta substituirmos esses valores na equação da partícula!
Passo 2
Para esboçarmos a trajetória da partícula vamos, inicialmente, de abrir a equação vetorial nas suas componentes:
Vamos fazer algumas manobras algébricas aqui. Como , vamos substituir na equação do :
Assim, a trajetória será no plano .
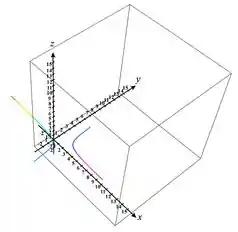
Passo 3
Quando se aproxima de pela direita, podemos perceber pelo gráfico que a partícula começa a ir para o mais infinito, enquanto . Se a aproximação for feita pela esquerda, podemos perceber pelo gráfico que a partícula começa a ir para o menos infinito.
Resposta
- e .
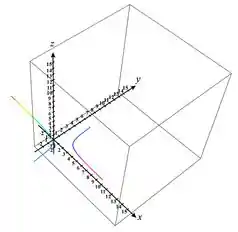
- A partícula tende para uma posição infinita.
Exercícios de Livros Relacionados
Mostre que κ e τ são ambos zero para a reta r t = x 0 + A t i + y 0 + B t j + z 0 + C t k
Nos Exercícios 7 e 8, encontre r , T , N e B no valor dado de t. Em seguida, encontre equações para os planos osculador, normal e retificador naquele valor de t.7. r t = cos t i + sen t j + k , t
Um objeto de massa m se move ao longo da parábola y = x 2 com um módulo de velocidade constante de 10 unidades/s. Qual é a força sobre o objeto decorrente de sua aceleração em ( 0,0 ) ? E em ( 2 1 2 ,
Nos Exercícios 7 e 8, encontre r , T , N e B no valor dado de t. Em seguida, encontre equações para os planos osculador, normal e retificador naquele valor de t.7. r t = cos t i + sen t j - k , t
Seja r → uma função vetorial derivável de t . Mostre que se r → ⋅ d r → / d t = 0 para todo t , então | r → | é constante.