Os exercícios de 99 e 100 referem-se à Secção Suplementar 2.10.
100) Dada .
(a) Determine os valores de k tais que ,
(b) Ache todos os intervalos abertos (a,b) contendo um valor de k que satisfaça a parte (a) tal que para todo em (a,b).
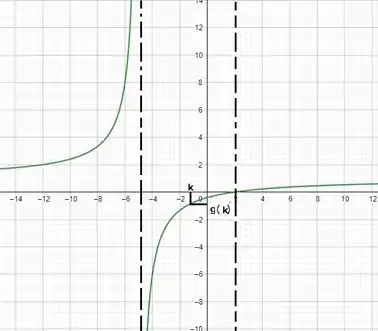
(c) Faça um esboço do gráfico de f e mostre no gráfico a interpretação geométrica dos resultados das partes (a) e (b).
Passo 1
a) Para temos:
Queremos encontrar os valores de k para os quais
Resolvendo a desigualdade encontramos:
Logo, , sempre que k estiver no intervalo:
b) Como f(x) >0 se e somete se -5
c)
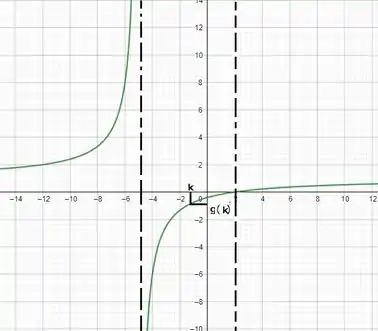
Resposta
- e
- Gráfico: