Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 3
Nos exercícios de 1 a 4, (a) ache a equação da parábola tendo o foco e a diretriz dados, (b) ache o comprimento do latus rectum e (c) faça um esboço da parábola.
3.Foco em ; diretriz,
Passo 1
(a) Para toda parábola com foco em , a equação será escrita assim:
Como a diretriz é e a equação da diretriz é
Então
Substituindo na equação da parábola:
Passo 2
Na letra (b) o enunciado pede o comprimento do latus rectum, chamaremos de c, que é dado por:
Substituindo o valor de p:
Passo 3
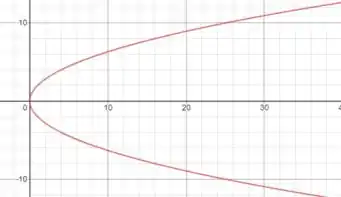
(c) Como , a nossa parábola abre-se para a direita e o esboço do gráfico é:
Resposta
Exercícios de Livros Relacionados
Encontre uma equação para a cônica que satisfaz as condições dadas35. Parábola, vértice ( 0,0 ) , eixo no eixoX , passando por ( 1 , - 4 )
Encontre uma equação para a cônica que satisfaz as condições dadas32. Parábola, vértice 1,0 , diretriz x = - 5
Encontre uma equação para a cônica que satisfaz as condições dadas31. Parábola, vértice 0,0 , foco ( 0 , - 2 )
Encontre uma equação para a cônica que satisfaz as condições dadas34. Parábola, foco 3,6 , vértice ( 3,2 )
Encontre uma equação para a cônica que satisfaz as condições dadas33. Parábola, foco - 4,0 , diretriz x = 2